11 Giugno 2007

Per arrivare alla sufficienza occorre rispondere alle domande non asteriscate.

Esercizio 1
Supponiamo fissato nello spazio euclideo un sistema di riferimento (0,i,j,k) e sia, al variare del parametro a, W_a la giacitura del piano che, nel dato riferimento, ha equazione.

a) Possono esistere in W_a per qulache valore di a, tre vettori linearmente indipendenti?
b) Detrminare una base di W_a
c)* Calcolare W₁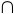W_-1 ( W₁ è la giacitura del piano relativo al valore del parametro a=1, mentre W_-1 quella relativa al valore a=-1.
Soluzione

Esercizio 2
Consideriamo in R⁴ i seguenti sottospazi vettoriali
U = Span((-1,-1,-1,-1),(1,1,1,1),(3,3,3,3),(-1/2,-1/2,-1/2,-1/2))
V = Span((-2,3,3,3),(0,1,1,1),(1,0,0,0),(2,1,1,1))
W = Span((1,3,1,1),(1,1,1,4),(0,1,0,2),(0,-1,0,0))

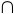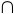a) Calcolare le dimensioni di U,V,W e una base per UVW.
b)* Rappresentare con un diagramma di Venn gli insiemi corrispondenti ai tre sottospazi.
Soluzione

Esercizio 3
Dare la definizione di cono circolare retto
Soluzione

Esercizio 4
Supponiamo fissato nello spazio euclideo un sistema di riferimento (0,i,j,k).
Consideriamo i 4 piani di equazioni 2x-y=a
x+y+az=0
x-2y-az=a
3ay+8z+4=0

a) Dare una condizione necessaria e sufficiente in termini di matrici affinché questi 4 piani si intersechino lungo una retta.
b) Determinare i valori del parametro a per i quali i 4 piani si intersecano lungo una retta e, per quei valori, calcolare la direzione di questa retta.
Soluzione