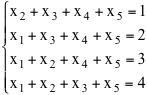31 Gennaio 2007
Per arrivare alla sufficienza occorre rispondere alle domande non asteriscate.
Esercizio 1
Dare la definizione di angolo tra due vettori numerici a n componenti.
Soluzione
Esercizio 2
Consideriamo i cinque vettori numerici a 4 componenti
u1 = (0,0,1,1), u2 = (1,2,-1,0), u3 =(1,3,1,2), u4 = (0,2,2,2) ,u5 = (0,0,2,2)
Calcolare la dimensione dello spazio V = Span(u1,u2,u3,u4,u5)
*Quali combinazioni lineari di e1 e di e2 appartengono a V? (e1 e e2 cono i primi due vettori della base canonica di R4.
Soluzione
Esercizio 3
Consideriamo le rette r e s definite dalle equazioni
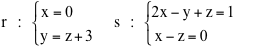
dire se le rette sono sghembe o complanari.
Sia Vr la direzione di r, cio è lo spazio vettoriale dei vettori geometri di r e Vs la direzione di s. Calcolare la dimensione dello spazio vettoriale Vr + Vs.
*In generale come si interpreta geometricamente la dimensione di Vr + Vs?
Soluzione
Esercizio 4
Descrivere tutte le soluzioni del seguente sistema di equazioni lineari
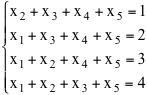
e dire se esiste una soluzione in numeri interi positivi. In caso affermativo esplicitarla.
* Dato un sistema lineare non omogeneo di m equazioni in n incognite compatibile, quando si può essere certi che il sistema ammette due diverse soluzioni?
Soluzione