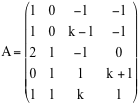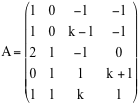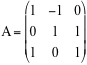31 Gennaio 2008

Le domande asteriscate sono più difficili e sono utili per valutare eventuali prove di eccellenza. .

Esercizio 1
Dare la definizione di sottospazio vettoriale.
Esercizio 2
Consideriamo la matrice

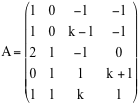
a)* Calcolare in funzione di k il rango della matrice A.
b)* Sia L_A l'applicazione lineare definita dalla matrice A. Dire quale è il dominio e quale il codominio di L_A e calcolare la dimensione della sua immagine.
c) Se A è una matrice i cui coefficienti dipendono con continuità da un parametro reale k e se per ogni valore di k non nullo il rango della matrice è r, cosa possiamo dire sul rango della matrice quando k=0?
Soluzione

Esercizio 3
Fissato nello spazio euclideo un sistema di riferimento cartesiano (O,i,j,k) sia 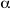il piano di equazione x+y+z=1 ed r la retta di equazioni cartesiane

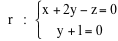
a)* Determinare una base ortonormale per la giacitura W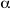 del piano .
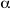b)*Calcolare le coordinate del punto A dove la retta r incontra il piano 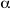e l'equazione cartesiana del piano che contiene r perpendicolare ad .
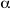c) Determinare il coseno dell'angolo tra la retta r e il piano 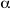. (Si ricorda che l'angolo tra una retta e un piano è l'angolo che la retta forma con la sua proiezione ortogonale sul piano)
Soluzione

Esercizio 4
Sia V lo spazio vettoriale formato dalle matrici con 3 righe e 2 colonne.
a)* Calcolare la dimensione di V e una sua base
b)* sia A la seguente matrice

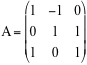
e U il sottospazio di V dato da tutte le matrici X tali che AX ¶ la matrice nulla. Calcolare la dimensione di U e una sua base.
c) Se A è una fissata matrice nxn di rango r e V lo spazio delle matrici nxm. Quale è la dimensione dello spazio

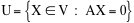
Soluzione