|
Lezioni di geometria Esercizi elementari |
 |
Gli esercizi che seguino sono di livello basso e permettono allo studente di verificare se la sua preparazione all'esame è sufficiente. Per questo bisogna che questi esercizi siano fatti con rapidità e senza incertezze. Alcuni esercizi dipendono da un parametro k e vanno risolti scegliendo un particolare valore per il parametro. Nelle soluzioni che abbiamo date, abbiamo scelto il valore k=1. Se lo studente ha incertezze su un certo esercizio può replicarlo per altri valori di k controllando la sua preparazione. Nelle soluzioni si rimanda ai paragrafi teorici che si debbono assimilare per un corretto svolgimento dell'esercizio.
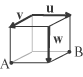 AB =............................ Soluzione 2. Dati i 4 vettori numerici di R5 : u1=(1,2,3,4,0) , u2=(4,1,2,3,0) , u3=(3,4,1,2,0) u4=(2,3,4,1,k) calcolare u1 + u2 + u3 + u4 = .......................................... Soluzione 3. Supponedo che la figura rappresenti un quadrato di lato unitario calcolare il prodotto scalare (-5u).v (-5u).v........................ Soluzione 4. Fissato un sistema di riferimento cartesiano nello spazio, scrivere le equazioni parametriche l'equazione cartesiana del piano parallelo al piano di equazione 2x-z=k e passante per il punto A=(k,-1,1). Soluzione 5. Posto a=k, ridurre con l'algoritmo di Gauss la matrice A indicando i pivot scelti, la matrice ridotta e il rango di A. 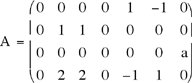 Soluzione 6. Sia V il sottospazio di R4 formato dai vettori numerici x = (x1, x2, x3, x4) di R4 tali che Determinare la dimensione di V e una sua base di V. Soluzione 7. Posto a=k, determinare i valori del parametro t affinchè il seguente sistema lineare non omogeneo sia compatibile 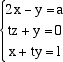 Soluzione 8. Data la matrice A calcolare, posto a=k, le prime 5 potenze di A, cioé A, A2, A3, A4, A5. Soluzione 9.Sia i , j , k una base ortonormale per i vettori geometrici dello spazio euclideo, consideriamo i vettori u=ki+ k , v=j + k , w=i- j. Calcolare il volume del parallelepipedo che ha per spigoli tre segmenti orientati equipollenti a u , v, w. Soluzione 10. Sia F = {0,1} il campo finito con due elementi (1+1=0) e sia A la matrice 3x3 a coefficienti in F le cui righe sono rispettivamente i numeri 3 (0,1,1), 5 (1,0,1), 7 (1,1,1) scritti in base 2. Calcolare la matrice A-1 inversa di A e dire quali numeri in base 10 corrispondono alle sue righe. Soluzione 11. Sia V lo spazio vettoriale formato dalle matrici 2x2. (La somma di "vettori" è la somma ordinaria di matrici, mentre il prodotto di una marice per uno scalare si esegue moltiplicandio tutti i coefficienti della matrice per lo scalare). Sia f l'operatore lineare V di in V che trasforma la generica matrice X di V in AX essendo A la matrice Calcolare una base per il nucleo di f. Soluzione |