Esercizi

Esercizio 1
Consideriamo i vettori numerici a 6 componenti u= (1,-1,0,0,1,1) , v= (2,-6,-2,-2,4,4) w=(1,1,1,1,0,0). Calcolare la dimensione dello spazio V= Span(u,v,w) e una sua base.
Soluzione

Esercizio 2
Consideriamo i tre vettori numerici a tre componenti u= (1,11,-1), v=(0, 8,-1) w=(1,3,0). Sia V il sottospazio R³ che essi generano: V= Span(u,v,w).
(a) Calcolare la dimensione di V.
(b) Determinare una base ortonormale di V.
Soluzione

Esercizio 3
1. Dire perché i seguenti 4 vettori di R² sono linearmente dipendenti

2. consideriamo lÕinsieme delle combinazioni lineari nulle di questi 4 vettori
a u + b v +c w + d z = 0 e pensiamo i 4 coefficienti di queste combinazioni lineari come vettori numerici (a,b,c,d) di R⁴.
(a) Scrivere con una formula matematica l'insieme di tutte queste quaterne.
(b) L'insieme descritto in (a) è uno spazio vettoriale. Calcolare una sua base e la sua dimensione.
Soluzione

Esercizio 4
Consideriamo i tre vettori numerici a tre componenti u=(1,1,1) , v = (1,-1,2) , w =(1,7,k). Sia V=Span(u,v,w) il sottospazio vettoriale R³ che essi generano. Determinare i valori di k (se esistono) per i quali dim V = 2.
Soluzione

Esercizio 5
Sia O un fissato punto dello spazio euclideo e sia i , j , k una base ortonormale dello spazio dei vettori geometrici. Consideriamo i tre punti dello spazio A, B, C tali che OA = i, OB = 2j, OC =3k e sia 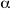il piano che contiene questi tre punti.
(a) Rappresentare con una figura la situazione descritta.
(b) Determinare una base per la giacitura W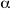 di quel piano.
Soluzione

Esercizio 6
Assegniamo un numero reale ad ogni vertice di un cubo in modo che la somma dei numeri su ogni faccia sia costante. Una volta ordinati i vertici del cubo ogni tale assegnazione é un vettore numerico a 8 componenti. LÕinsieme V di tutti questi vettori forma un sottospazio vettoriale di R⁸. Valutare la dimensione di V.
Soluzione

Esercizio 7 (Esercizio assegnato all'esame del 19 Settembre 2007)
In R⁵, dotato del prodotto scalare usuale, si considerino il vettore v=(1,0,1,0,-1) ed il sottospazio vettoriale W formato dai vettori (x₁,x₂,x₃,x₄,x₅) tali che x₁-x₂+x₃+x₅ = 0 1. Verificare se il vettore v appartiene a W.
2. Determinare una base ortonormale di W e completarla ad una base di R⁵.
3*. Determinare un vettore w apartenente a W e un vettore w' appartenete allo spazio ortogonale di W tali che v = w + w'.
Soluzione

Esercizio 8 (Esercizio assegnato all'esame del 3 Febbraio 2007)
Nello spazio R⁴ dei vettori numerici a 4 componenti sia W il sottospazio delle soluzioni delle equazioni: x₁ + 3x₂ - x₃ = 0
2x₃ + x₄ = 0 Sia inoltre U il più piccolo sottospazio contenete W e i vettori u₁=(1,0,-1,0) e u₂=(2,3,0,-2). Determinare la dimensione di U e una sua base ortonormale.
Soluzione