|
I. 1 La geometria dello spazio euclideo
Questo capitolo ho lo scopo di introdurre gli allievi ai metodi della geometria, alle sue tecniche dimostrative, alle sue iniziali definizioni seguendo sostanzialmente il percorso indicato da
Euclide nel XI libro degli Elementi
1.
Il procedimento deduttivo pone al principio dei postulati e delle definizioni a partire dai quali vengono dedotti, col ragionamento sillogistico, dei teoremi secondo un determinato ordine che permette di usare i teoremi già dimostrati per costruire nuove dimostrazioni e nuovi teoremi. I postulati fissano alcune relazioni tra enti primitivi che vengono accettate come vere senza bisogno di dimostrazione. Gli enti primitivi sono oggetti astratti della teoria che hanno un corrispettivo nel mondo reale o nella nostra immaginazione. Gli enti primitivi nel nostro caso sono: punto, retta, piano, spazio, angolo. Le definizioni danno un nome ad nuovi enti definiti univocamente a partire da quelli. Troviamo all'inizio degli Elementi 23 definizioni. Ad esempio la definizione X dice testualmente
- Definizione X
quando una retta innalzata su un'altra retta forma degli angoli adiacenti uguali tra loro, ciascuno dei due angoli uguali è retto e la retta innalzata si chiama perpendicolare a quella su cui è innalzata.
Seguono la definizione di circonferenza, di diametro, di triangolo, di quadrilatero e infine
- Definizione XXIII
Parallele sono quelle rette che essendo in uno stesso piano e venendo prolungate illimitatamente dall'una e dall'altra parte non si incontrano tra loro da nessuna delle due parti.
I 5 postulati iniziali di Euclide dicono testualmente
Risulti postulato:
- che si possa condurre una linea retta da un qualsiasi punto ad ogni altro punto
- e che una retta terminata si possa prolungare continuamente in linea retta
- e che si possa descrivere un cerchio con qualsiasi centro e ogni distanza
- e che tutti gli angoli retti siano uguali tra loro
- e che se una retta venendo a cadere su altre due rette forma angoli interni e dalla stessa parte minori di due retti, le due rette prolungate illimitatamente verranno ad incontrarsi da quella parte in cui sono gli angoli minori di due retti.

La geometria dello spazio come abbiamo detto è introdotta da Euclide nel XI libro. Vi sono 28 definizioni delle quali ricordiamo quelle essenziali per la trattazione successiva. Altre saranno riprese più avanti. Queste definizioni vanno imparate a memoria: sono gli atomi iniziali di un linguaggio scientifico col quale è possibile costruire poi un discorso dimostrativo razionale.
- Definizione III
Una retta è perpendicolare a un piano quando forma angoli retti con tutte le rette che la incontrano e che siano su quel piano.
- Definizione VIII
Sono paralleli i piani che non si incontrano
Per rappresentare con una immagine la definizione di perpendicolarità tra rette e piani possiamo pensare alle "zampe di gallina"
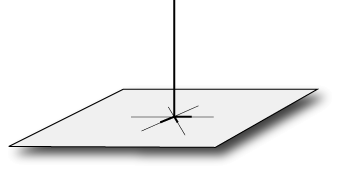
La geometria dello spazio ha bisogno di altri tre postulati che nel testo euclideo si trovano all'inizio del libro XI nella forma di teoremi. In realtà le "dimostrazioni" di queste proposizioni sono non rigorose e si fondano su elementi fortemente intuitivi. Tenendo conto che il testo originale di Euclide, come un tempio antico, è pervenuto fino a noi dopo successivi rimaneggiamenti e copie manoscritte via via corrotte da commenti, note "esplicative", aggiunte, molti storici ritengono che quelle "dimostrazioni" siano in realtà dei commenti spuri aggiunti per dare una qualche giustificazione dei nuovi postulati.
Essi sono
- Postulato I
Se due o più punti di una retta stanno su un piano tutta la retta è contenuta in quel piano

In formule
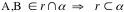
- Postulato II
Per tre punti che non stanno su una retta passa uno e un solo piano

- Postulato III
Se due piani distinti si incontrano hanno in comune una retta.
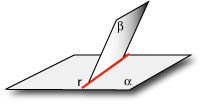
In formule
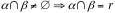
Notiamo che i postulati I e II implicano la proposizione seguente
Proposizione 1
Due rette che si incontrano in un punto giaciono su uno e un solo piano.
La dimostrazione di questa proposizione è diretta e naturale.
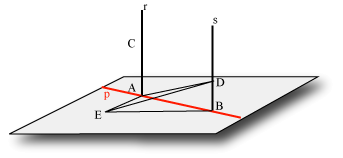
Sia A il punto d'intersezione delle rette r ed s. Sia B un punto di r diverso da A e C un punto di s diverso da A. Dato che le due rette sono diverse, i punti A,B,C non sono allineati dunque, per il postulato II, esiste uno e un solo piano che passa per A,B,C. Dato che A e B stanno anche sulla retta r e B è diverso da A, per il postulato I tutta la retta r è contenuta in quel piano. Si ragiona analogamente per la retta s.
La figura seguente illustra i passi della dimostrazione
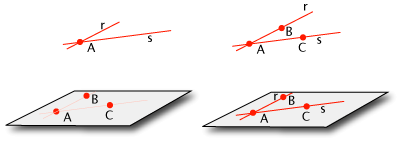
Notiamo che due rette generiche dello spazio non stanno su uno stesso piano: questo accade se e solo se le due rette sono parallele (per la definizione di parallelismo) o, come abbiamo visto, se le due rette si intersecano in un punto. Due rette che stanno su uno stesso piano si dicono complanari mentre si dicono sghembe quando questo non accade.
Possiamo ora dimostrare qualche teorema seguendo testualmente la trattazione euclidea.
Teorema 1 (Euclide, Elementi XI,4)
Se una retta è innalzata perpendicolarmente al comune punto di intersezione di due rette che si tagliano tra loro essa sarà perpendicolare al piano che passa per esse.
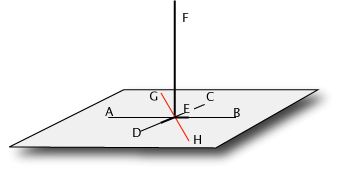
Supponiamo che, per ipotesi, la retta EF sia perpendicolare alle rette AB e CD e che queste rette si incontrino in E. Per il postulato II esiste un piano e uno solo che contiene A,E,C, e quindi per il postulato I le rette AEB e CED. Si deve dimostrare che questo piano è perpendicolare alla retta EF. Per dimostrare questo, dato che, per definizione, una retta è perpendicolare a un piano nel punto E se è perpendicolare ad ogni retta del piano passante per E, si deve dimostrare che EF è perpendicolare a ogni retta del piano passante per E. Sia GH una qualunque di queste rette. Dobbiamo dunque dimostrare che gli angoli GEF e HEF sono uguali. Per fare questo costruiamo la seguente figura
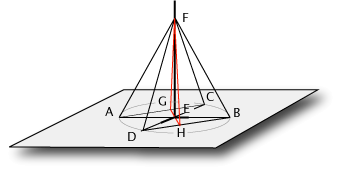
Costruiamo i segmenti uguali AE=EB=CE=DE.
Ora si ragiona con lo scopo di dimostrare che i triangoli HEF e GEF sono uguali. Per fare questo cerchiamo di dimostrare che questi due triangoli hanno i lati uguali.
-
I triangoli AEC e BED sono uguali avendo uguali due lati e l'angolo compreso. In particolare sono isosceli e hanno gli angoli alla base uguali
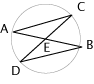
- I triangoli CEG e DEH sono uguali dato che hanno gli angoli uguali e il lato EC=ED. In particolare EH = EG.

- AF = BF = CF = DF perché i triangoli AEF, BEF, CEF e DEF sono tutti uguali tra loro avendo uguali i lati AE,BE,CE,DE per costruzione il lato EF che è in comune e gli angoli AEF, BEF, CEF e DEF che sono retti per ipotesi. In particolare i triangoli ACF e BDF sono uguali perché hanno uguali i tre lati. Ne segue che gli angoli FDB e FCA sono uguali tra loro.
- I triangoli DHF e CGF sono uguali perché hanno uguali DH=CG, DF = CF e l'angolo FDH e FCG. In particolare FH = FG.
Questo teorema, in particolare, implica che una retta perpendicolare a un piano non può stare su quel piano dato che una retta non può essere perpendicolare a se stessa. Una retta perpendicolare a un piano sta fuori da quel piano, occupa uno spazio più grande, definisce una nuova direzione "verso fuori" che non si trova tra le infinite direzioni del dato piano.
Il teorema seguente fissa a tre la dimensione dello spazio stabilendo che non possono esserci più di tre direzioni a due a due ortogonali tra loro.
Teorema 2 (Euclide, Elementi XI,5)
Se una retta è innalzata perpendicolarmente nel comune punto di intersezione di tre rette che si incontrano tra loro, allora le tre rette stanno su uno stesso piano.
Siano BC,BD,BE le tre rette e supponiamo che la retta AB sia perpendicolare a tutte e tre. Vogliamo dimostrare che allora le tre rette stanno su un piano cioè che i quattro punti B,C,D,E sono complanari.
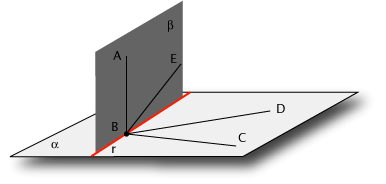
Sia  il piano che contiene i punti B,C,D e il piano che contiene i punti B,C,D e  il piano che contiene i punti A,B,E. Tali piani esistono e sono unici per il postulato II. I due piani il piano che contiene i punti A,B,E. Tali piani esistono e sono unici per il postulato II. I due piani  e e  non sono uguali. Infatti la retta AB essendo perpendicolare sia a BC che BD è perpendicolare, per il teorema 1, al piano non sono uguali. Infatti la retta AB essendo perpendicolare sia a BC che BD è perpendicolare, per il teorema 1, al piano  e quindi non può stare su quel piano. I piani e quindi non può stare su quel piano. I piani  e e  non sono neppure paralleli dato che hanno in comune almeno il punto B. Essi dunque si intersecano, per il postulato III, in una retta. Sia r tale retta. Vogliamo dimostrare che la retta r è uguale alla retta BE. Ciò deriva dal fatto che r si trova sul piano non sono neppure paralleli dato che hanno in comune almeno il punto B. Essi dunque si intersecano, per il postulato III, in una retta. Sia r tale retta. Vogliamo dimostrare che la retta r è uguale alla retta BE. Ciò deriva dal fatto che r si trova sul piano  e dunque, per il teorema 1, è perpendicolare alla retta AB. Ma r si trova anche sul piano e dunque, per il teorema 1, è perpendicolare alla retta AB. Ma r si trova anche sul piano  e in quel piano anche BE è perpendicolare alla retta AB. Dato che in un piano esiste una e una sola retta perpendicolare ad AB nel punto B, deve essere r uguale alla retta BE. e in quel piano anche BE è perpendicolare alla retta AB. Dato che in un piano esiste una e una sola retta perpendicolare ad AB nel punto B, deve essere r uguale alla retta BE.
Teorema 3 (Euclide, Elementi XI,8)
Se due rette sono parallele e una è perpendicolare a un piano allora anche l'altra è perpendicolare a quel piano
Detto in modo più formale, il teorema afferma che,
r perpendicolare ad  , s parallela a r implica s perpendicolare ad , s parallela a r implica s perpendicolare ad  . .
Introducendo un simbolo per la relazione di perpendicolarità e per quella di parallelismo, l'enunciato precedente si scrive
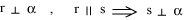
La formula mette in evidenza la struttura logica dell'enunciato. La proposizione è fatta di tre enunciati semplici:
r perpendicolare ad  , r parallela a s e s perpendicolare ad , r parallela a s e s perpendicolare ad  . Si tratta di dimostrare che, assumendo come veri i primi due enunciati, risulta necessariamente il terzo. Per dimostrare che s perpendicolare ad . Si tratta di dimostrare che, assumendo come veri i primi due enunciati, risulta necessariamente il terzo. Per dimostrare che s perpendicolare ad  dobbiamo riprendere la definizione di perpendicolarità tra rette e piani: dobbiamo quindi dimostrare che s è perpendicolare ad ogni retta del piano passante per il punto B dove s incontra dobbiamo riprendere la definizione di perpendicolarità tra rette e piani: dobbiamo quindi dimostrare che s è perpendicolare ad ogni retta del piano passante per il punto B dove s incontra  .
Poiché queste rette sono infinite sembrerebbe necessario fare una infinità di dimostrazioni una per ogni retta, cosa ovviamente impossibile. E' a questo punto che ci viene in aiuto il teorema 1: basta dimostrare che s è perpendicolare a due rette di .
Poiché queste rette sono infinite sembrerebbe necessario fare una infinità di dimostrazioni una per ogni retta, cosa ovviamente impossibile. E' a questo punto che ci viene in aiuto il teorema 1: basta dimostrare che s è perpendicolare a due rette di  passanti per B perché allora è perpendicolare anche a tutte le altre. passanti per B perché allora è perpendicolare anche a tutte le altre.
Euclide costruisce due particolari rette per le quali è capace di dimostrare la perpendicolarità con r. Per fare questo Euclide inventa un utilissimo "strumento geometrico" in grado di traslare angoli nello spazio. Cominciamo col descrivere questo strumento
Figura animata 1
Consideriamo un triangolo ABD su un dato piano e un triangolo ABC uguale a quello su un'altro piano incernierato lungo la retta AB. Se ruotiamo il piano del triangolo ABC nello spazio, cosa che è possibile fare muovendo il punto C, si vengono a formare comunque sia la rotazione effettuata, due triangoli che hanno i tre lati uguali (CA=BD, AD=BC) e che quindi sono uguali: il triangolo CAD e il triangolo CBD. In questo modo l'angolo CAD risulta uguale all'angolo CBD.
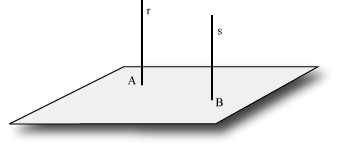
Per dimostrare il teorema usiamo questa costruzione nel modo seguente. Dato che le rette r ed s sono parallele per ipotesi, esse stanno su un piano  che interseca il piano che interseca il piano  lungo una retta p. Poiché r è perpendicolare al piano lungo una retta p. Poiché r è perpendicolare al piano  per ipotesi, la retta p è perpendicolare alla retta r. Ne segue che, essendo r ed s parallele per ipotesi, anche la retta s è perpendicolare alla retta p. per ipotesi, la retta p è perpendicolare alla retta r. Ne segue che, essendo r ed s parallele per ipotesi, anche la retta s è perpendicolare alla retta p.
Dobbiamo ora dimostrare, ricordando la definizione di perpendicolarità tra retta e piano, che s è perpendicolare a una qualunque retta di  passante per B. passante per B.
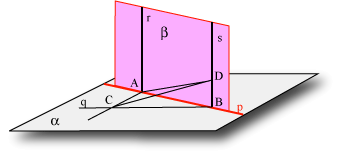
Sia dunque q una generica retta passante per B. Intersechiamo questa retta con la retta per A perpendicolare a p. Sia C il punto di intersezione. Costruiamo ora un segmento BD = AC. I due triangoli ABC e ABD sono uguali tra loro essendo entrambi rettangoli (l'angolo DBA è retto perché s è perpendicolare a p) e con uguali cateti. Usando ora il nostro "strumento geometrico" possiamo dedurre che l'angolo DBC è uguale all'angolo CAD. Ma quest'angolo è rettangolo dato che CA è perpendicolare a p e a r e dunque, per il teorema 1, è perpendicolare al piano  e quindi è perpendicolare a tutte le rette di quel piano passanti per A e, in particolare, alla retta AD. Essendo gli angoli CAD = DBC rettangoli, la retta s risulta perpendicolare a p e a BC e dunque perpendicolare al piano e quindi è perpendicolare a tutte le rette di quel piano passanti per A e, in particolare, alla retta AD. Essendo gli angoli CAD = DBC rettangoli, la retta s risulta perpendicolare a p e a BC e dunque perpendicolare al piano  . .
Il teorema seguente è in un certo senso l'inverso del precedente
Teorema 4 (Euclide, Elementi XI,6)
Se due rette sono perpendicolari allo stesso piano sono parallele tra loro.
Le ipotesi ora sono che r ed s sono perpendicolari ad  e la tesi è che allora le due rette sono parallele. In modo simbolico l'enunciato si scrive e la tesi è che allora le due rette sono parallele. In modo simbolico l'enunciato si scrive
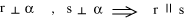
Questo enunciato non è l'inverso del precedente perché l'ipotesi che
r sia perpendicolare ad  è comune ai due enunciati: la tesi dunque non si cambia con l'ipotesi come avviene in enunciati l'uno inverso dell'altro. In ogni caso possiamo riunire i due enunciati in un unico enunciato nel modo seguente è comune ai due enunciati: la tesi dunque non si cambia con l'ipotesi come avviene in enunciati l'uno inverso dell'altro. In ogni caso possiamo riunire i due enunciati in un unico enunciato nel modo seguente
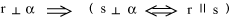
Il nuovo simbolo introdotto, la doppia freccia, si legge se e solo se e tutto l'enunciato si legge: se r è perpendicolare ad  allora s è perpendicolare ad allora s è perpendicolare ad  se e solo se s è parallela a r.
L' espressione simbolica contiene in forma estremamente compatta gli enunciati dei teoremi XI,6 e XI,8 degli Elementi di Euclide. L'efficacia della matematica consiste anche nella sua capacità di condensare in un linguaggio simbolico preciso enunciati anche molto complessi, enunciati che, in questo modo, possono essere trasferiti su un calcolatore elettronico e manipolati automaticamente. Oltre al linguaggio formale è molto importante formarsi una immagine mentale isomorfa al contenuto della proposizione. Questa immagine permette di ricordare e capire meglio il significato della proposizione e il suo utilizzo in atri contesti. In questo caso possiamo ad esempio rappresentare una retta perpendicolare a un piano come una "zampa di gallina" e due rette parallele evidenziando che stanno su un piano e che formano angoli retti con una trasversale. L'immagine potrebbe essere questa. se e solo se s è parallela a r.
L' espressione simbolica contiene in forma estremamente compatta gli enunciati dei teoremi XI,6 e XI,8 degli Elementi di Euclide. L'efficacia della matematica consiste anche nella sua capacità di condensare in un linguaggio simbolico preciso enunciati anche molto complessi, enunciati che, in questo modo, possono essere trasferiti su un calcolatore elettronico e manipolati automaticamente. Oltre al linguaggio formale è molto importante formarsi una immagine mentale isomorfa al contenuto della proposizione. Questa immagine permette di ricordare e capire meglio il significato della proposizione e il suo utilizzo in atri contesti. In questo caso possiamo ad esempio rappresentare una retta perpendicolare a un piano come una "zampa di gallina" e due rette parallele evidenziando che stanno su un piano e che formano angoli retti con una trasversale. L'immagine potrebbe essere questa.

Vediamo ora come si dimostra il teorema 4. Come prima cosa si tratta di capire bene quali sono le ipotesi e cosa si vuole dimostrare e poi bisogna cercare un'idea (e qua si esplica la creatività del matematico) per dimostrare la tesi. Per ipotesi le due rette r ed s sono perpendicolari al piano
 e dobbiamo dimostrare che allora sono parallele. Siano A e B i punti in cui le rette incontrano il piano, e siano C e D altri due punti sulle rette r ed s rispettivamente. Sia p la retta che congiunge A con B. e dobbiamo dimostrare che allora sono parallele. Siano A e B i punti in cui le rette incontrano il piano, e siano C e D altri due punti sulle rette r ed s rispettivamente. Sia p la retta che congiunge A con B.
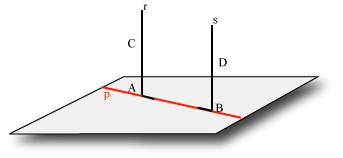
Dato che sia r che s sono perpendicolari al piano  , esse saranno perpendicolari alla retta p. Basta allora dimostrare che le due rette sono su uno stesso piano (due rette sono parallele per definizione se sono su uno stesso piano e non si incontrano), perché, in questo caso, formando con la trasversale p angoli retti, per il V postulato, non possono incontrarsi.
Per dimostrare che le due rette sono su uno stesso piano dimostriamo che le tre rette AC,AB,AD sono complanari cercando di utilizzare il teorema 2. Per fare questo (ecco l'idea!) usiamo il nostro "strumento geometrico" costruendo una retta ausiliaria AE e dimostrando che questa retta ausiliaria è perpendicolare ad AB, AC e AD. La conclusione segue a questo punto usando il teorema 2. , esse saranno perpendicolari alla retta p. Basta allora dimostrare che le due rette sono su uno stesso piano (due rette sono parallele per definizione se sono su uno stesso piano e non si incontrano), perché, in questo caso, formando con la trasversale p angoli retti, per il V postulato, non possono incontrarsi.
Per dimostrare che le due rette sono su uno stesso piano dimostriamo che le tre rette AC,AB,AD sono complanari cercando di utilizzare il teorema 2. Per fare questo (ecco l'idea!) usiamo il nostro "strumento geometrico" costruendo una retta ausiliaria AE e dimostrando che questa retta ausiliaria è perpendicolare ad AB, AC e AD. La conclusione segue a questo punto usando il teorema 2.
In dettaglio costruiamo sul piano  una retta AE perpendicolare alla retta AB e tale che AE = BD. Abbiamo una retta AE perpendicolare alla retta AB e tale che AE = BD. Abbiamo
-
AE perpendicolare a AB per costruzione
- AE perpendicolare ad AC perché la retta AC è perpendicolare al piano
 per ipotesi per ipotesi
- AE è perpendicolare ad AD perché, usando lo "strumento geometrico", l'angolo EAD risulta uguale all'angolo DBE che è retto perché la retta DB è perpendicolare per ipotesi al piano
 . .
Concludiamo questo capitolo con la costruzione della retta perpendicolare.
Teorema 5 (Euclide, Elementi XI,11)
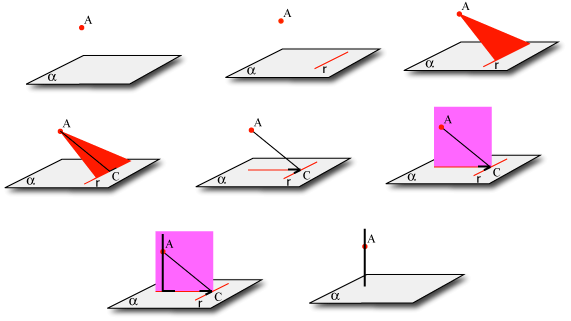
Da un punto dato fuori da un piano condurre una linea retta perpendicolare al piano.
Riportiamo la costruzione euclidea con una serie di immagini che descrivono passo a passo la costruzione. Questa costruzione si basa sul fatto noto di geometria piana: in un piano data una retta e un punto esiste una e una sola retta passante per quel punto e perpendicolare a quella retta.
I seguenti esercizi interattivi aprono una pagina di posta nella quale si deve scrivere come soggetto l'esercizio cui si riferisce e come testo la propria soluzione. Inviare il testo che sarà poi corretto, una volta a settimana, per posta elettronica
Esercizio interattivo 0.1
Scrivere verbalmente, con la massima precisione possibile, i vari passaggi della costruzione della perpendicolare descritti con le immagini precedenti giustificandone la correttezza sulla base dei postulati e di teoremi precedenti
Esercizio interattivo 0.2
Dimostrare che la retta costruita con i passaggi precedenti è perpendicolare al piano  . .
Esercizio interattivo 0.3Come costruire la retta per A perpendicolare al piano  quando il punto A si trova sul piano? quando il punto A si trova sul piano?
Il seguente teorema viene dimostrato per assurdo.
Teorema 6 (Euclide, Elementi XI,13)
Da uno stesso punto non possono innalzarsi due rette perpendicolari a uno stesso piano.
Supponiamo che il punto A stia sul piano  e supponiamo per assurdo che esistano due rette r ed r' passanti per A e perpendicolari al piano. e supponiamo per assurdo che esistano due rette r ed r' passanti per A e perpendicolari al piano.
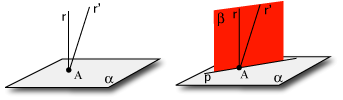
Considerando il piano  che contiene r ed r' . Tale piano esiste in virtù del postulato II. Il piano che contiene r ed r' . Tale piano esiste in virtù del postulato II. Il piano  non coincide col piano non coincide col piano  perché la retta r (e r') è perpendicolare ad perché la retta r (e r') è perpendicolare ad  . Sia dunque p la retta nella quale questo piano incontra il piano . Sia dunque p la retta nella quale questo piano incontra il piano  . Questa retta esiste in virtù del postulato III. Dato che r e r' sono perpendicolari ad . Questa retta esiste in virtù del postulato III. Dato che r e r' sono perpendicolari ad  , r e r' saranno perpendicolari a p dato che p passa per A e si trova sul piano , r e r' saranno perpendicolari a p dato che p passa per A e si trova sul piano  , ma questo è assurdo perché sul piano , ma questo è assurdo perché sul piano  non possono esistere due rette perpendicolari a una stessa retta per uno stesso punto A. Infatti queste eventuali due rette, formando angoli retti con la retta p, sarebbero parallele il che è assurdo, se sono diverse, perché hanno il punto A in comune
3. non possono esistere due rette perpendicolari a una stessa retta per uno stesso punto A. Infatti queste eventuali due rette, formando angoli retti con la retta p, sarebbero parallele il che è assurdo, se sono diverse, perché hanno il punto A in comune
3.
Lo stesso ragionamento vale anche se A non sta sul piano  . .
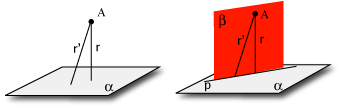
Notiamo che l'assurdo non dipende dal fatto che la conclusione è contraria al nostro buon senso o alla nostra intuizione ma dal fatto che la conclusione a cui siamo arrivati contraddice un teorema dimostrato precedentemente.
Esercizio interattivo 0.4
Dimostrare che due piani perpendicolari a una stessa retta sono paralleli (Elementi XI,14).
Studiamo ora la relazione di perpendicolarità riferita a due piani.
Cominciamo col dare la definizione di perpendicolarità tra piani, definizione che nel libro XI degli Elementi di Euclide ha il numero 4 e dice testualmente.
- Definizione IV
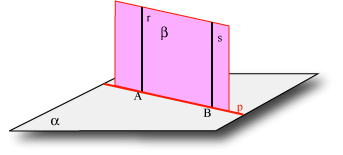
Una piano è perpendicolare a un'altro piano quando le rette condotte, in uno dei due piani, perpendicolarmente alla intersezione comune dei piani, sono perpendicolari all'altro piano
Siano  e e  i due piani che supponiamo non paralleli e sia p la retta nella quale si intersecano. Diciamo allora, per definizione, che i due piani che supponiamo non paralleli e sia p la retta nella quale si intersecano. Diciamo allora, per definizione, che  e perpendicolare ad e perpendicolare ad  se ogni retta di se ogni retta di  perpendicolare a p è perpendicolare ad perpendicolare a p è perpendicolare ad  . .
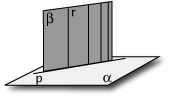
La definizione si scrive simbolicamente nel modo seguente
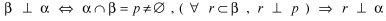
e si legge  è perpendicolare ad è perpendicolare ad  se e solo se se e solo se  intersezione intersezione  uguale a p è non vuoto e ogni retta r di uguale a p è non vuoto e ogni retta r di  perpendicolare a p è perpendicolare a perpendicolare a p è perpendicolare a 
.
Dato che le rette di  perpendicolari a p sono tutte parallele tra loro, per il teorema 3, basta che una retta di perpendicolari a p sono tutte parallele tra loro, per il teorema 3, basta che una retta di  sia perpendicolare a p affinché il piano sia perpendicolare a p affinché il piano  sia perpendicolare ad sia perpendicolare ad  . La definizione data è quindi equivalente a quest'altra definizione: . La definizione data è quindi equivalente a quest'altra definizione:
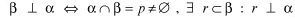
che si legge:
 è perpendicolare ad è perpendicolare ad  se e solo se se e solo se  intersezione intersezione  uguale a p è non vuoto ed esiste una retta r di uguale a p è non vuoto ed esiste una retta r di  perpendicolare a perpendicolare a  . .
I nuovi simboli introdotti (la A capovolta = per ogni e la E girata = esiste) si chiamano quantificatori e sono di enorme importanza in matematica. I due punti si usano generalmente nel significato di tali che.
Non è difficile dimostrare (vedi esercizi) che la relazione di perpendicolarità tra piani è simmetrica, cioè  è perpendicolare a è perpendicolare a  se e solo se se e solo se  è perpendicolare ad è perpendicolare ad 
Gli esercizi seguenti hanno lo scopo di esercitare l'allievo all'uso matematico della logica formale sviluppando le sue capacità di ragionamento.
Esercizi
| |





















