Infatti se au = 0 allora |au| =| a|.|u| = 0, ma abbiamo ora il prodotto di due numeri reali e questo prodotto è nullo se e solo se almeno uno dei due numeri è nullo. Dunque o a = 0 o |u| = 0 ma |u| = 0 se e solo se u = 0.

La definizione 1 si può riformulare dicendo che u è linearmente indipendente e se e solo se au = 0 implica a = 0.
Da un punto di vista più geometrico possiamo anche dire che un vettore u linearmente indipendente individua univocamente una direzione dello spazio infatti, essendo u non nullo, è rappresentato da un segmento orientato AB con A diverso da B e questo, a sua volta, definisce una direzione quella individuata dalla retta AB. In definitiva

• Un vettore geometrico u è linearmente indipendente se e solo se individua una direzione.

Dato un vettore u diciamo che v dipende linearmente da u se v = au, cioè se v è un multiplo di u. Dato che, se u ed a sono diversi da zero, il vettore au ha la stessa direzione del vettore u, se il vettore v è linearmente dipendente da u, allora u e v hanno la stessa direzione. Viceversa se u e v sono non nulli e hanno la stessa direzione allora v è linearmente dipendente da u. Questa seconda affermazione ci riporta al così detto assioma di continuità che viene generalmente trattato in tutti i suoi significati nei corsi di logica matematica. Infatti se i due vettori geometrici u e v hanno la stessa direzione, applicando questi due vettori a uno stesso punto O, abbiamo u= OU e v = OP e i tre punti O U e P risultano allineati essendo le due rette OU e OP parallele (due rette parallele con un punto in comune sono uguali). Per l'assioma di continuità dunque il rapporto OP : OU, comunque siano i punti O, U e P sulla retta, è un numero reale a che esprime v come multiplo di u secondo lo scalare a: v = au.

Nella figura precedente è v = -2u.

La negazione della dipendenza lineare conduce alla indipendenza lineare. Precisamente

Definizione 2
Diciamo che due ¹ vettori geometrici u e v sono linearmente indipendenti se la sola loro combinazione lineare nulla è quella banale².

Ciò significa che u e v sono linearmente indipendenti se e solo se

E' chiaro che, se v è linearmente dipendente da u allora i vettori u e v non sono linearmente indipendenti, perché, in questo caso, v = au e quindi

è una combinazione lineare nulla e non banale dei vettori u e v (con coefficienti a e -1) contraddicendo la definizione precedente di indipendenza lineare. Viceversa se i vettori u e v non sono linearmente indipendenti, cioé se esiste una loro combinazione lineare nulla e non banale, allora uno dei due vettori è linearmente dipendente dall'altro. Infatti se au + bv = 0 è la combinazione lineare non banale, allora almeno uno dei due coefficienti deve essere diverso da zero. Supponiamo che sia b non nullo. Possiamo allora con facili calcoli, possibili in virtù delle varie proprietà delle operazioni tra vettori, ricavare v in funzione di u. In questo caso riportiamo tutti i passaggi che rendono leggittimo il calcolo, nel seguito, essendo la situazione algebrica del tutto analoga a quella dell'aritmetica elementare, procederemo in modo più spedito.

dove il coefficiente t è l'opposto di a diviso b.

In definitiva due vettori non nulli non sono linearmente indipendenti se e solo se uno è dipendente dall'altro e questo accade se e solo se i due vettori hanno la stessa direzione. La negazione di quest'ultima condizione ci permette di caratterizzare geometricamente l'indipendenza lineare di due vettori geometrici.

• Due vettori geometrici u e v, sono linearmente indipendenti se e solo se individuano due direzioni diverse.

Infatti se i due vettori sono linearmente indipendenti nessuno dei due può essere nullo perché altrimenti, se ad esempio fosse u=0, allora 1u + 0v=0 sarebbe una combinazione lineare nulla e non banale contro la nostra ipotesi. I due vettori definiscono quindi due direzioni che non possono coincidere perché altrimenti sarebbero dipendenti. Viceversa se definiscono due direzioni distinte sono intanto non nulli e quindi, per quello che abbiamo detto, indipendenti.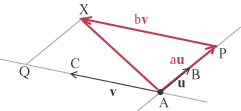

Cominciamo ora ad analizzare i possibili rapporti tra tre vettori geometrici. Per fare questo è molto utile la seguente definizione che generalizza la nozione di direzione.

Definizione
Diciamo che due piani hanno la stessa giacitura se sono paralleli.

La giacitura è, come la direzione, una classe di equivalenza. Ogni classe di equivalenza è formata da tutti i piani dello spazio paralleli a un dato piano che rappresenta la classe. Vedremo più avanti una definizione più formale di giacitura in termini di sottospaspazi vettoriali. La sola giacitura che ha un nome nella lingua corrente è quella orizzontale. In generale, mancando le parole per indicare i concetti, per dare una giacitura occorre indicare un rappresentante di quella giacitura cioé un piano e solo a questo punto possiamo parlare della giacitura rappresentata da quel particolare piano che abbiamo indicato.
Il fatto geometrico interessante è ora che, come un vettore linearmente indipendente definisce univocamente una direzione, cosí due vettori linearmente indipendenti definiscono univocamente una giacitura. Siano infatti u e v due vettori geometrici linearmente indipendenti, consideriamo un punto A dello spazio e applichiamo i due vettori nel punto A: essendo i due vettori non nulli, troveremo due segmenti orientati AB e AC con A,B,C non allineati, perché altrimenti i due vettori sarebbero linearmente dipendenti. I tre punti A, B, C individuano un unico piano e quindi una giacitura. La giacitura del piano per A, B, C è ovviamente definita a partire dal punto A e dai vettori u= AB e v=AC tuttavia essa non dipende da A ma solo dai due vettori. Se infatti A' è un'altro punto dello spazio e se A'B' e A'C' sono altri due segmenti orientati che rappresentano gli stessi vettori u e v allora, in virtù della proposizione XI, 15 di Euclide i due piani A,B,C e A', B', C' risultano paralleli essendo parallele le rette AB e A'B' e AC e A'C'. I due piani quindi definiscono la medesima giacitura. In definitiva dunque due vettori u e v e un punto A dello spazio definiscono un piano, cambiano il punto A cambia il piano ma non cambia la sua giacitura che viene così a dipendere solo da u e v.

Possiamo ora descrivere facilmente tutti i vettori geometrici ottenibili combinando linearmente due vettori indipendenti u e v. Sia w = au + bv. Per vedere le caratteristiche di w rappresentiamo i vettori con dei segmenti orientati. Fissiamo un punto A dello spazio e applichiamo i vettori in A. Abbiamo u = AB e v =AC con A, B. C non allineati perché u e v sono linearmente indipendenti.

Il vettore au = AP ha la stessa direzione di u e quindi il punto P si trova sulla retta AB, analogamente bv = AQ ha la stessa direzione di v e quindi il punto Q si trova sulla retta AC. La somma dei due vettori, cioé w = AX si troverà sul piano individuato da A, B, C dato che le rette AP e QX sono parallele e quindi complanari così che i punti A, P , Q , X stanno su uno stesso piano che è il piano individuato da A, B, C. Viceversa se X è un qualunque punto del piano individuato dai punti A, B, C, allora possiamo tracciare la parallela alla retta AC passante per X la quale interseca la retta AB nel punto P, dato che, in un piano due rette non parallele si incontrano e la retta per X con la direzione di v non ha la direzione di u essendo v e u linearmente indipendenti. Per costruzione dunque, il vettore PX ha la stessa direzione di v e quindi è un suo multiplo: PX = bv. Anche il vettore AP ha la stessa direzione di u e quindi AP = au. In definitiva AX = AP + PX = au + bv.
Concludiamo questa analisi dicendo che un vettore w dipende linearmente da due vettori linearmente indipendenti u e v se e solo se, applicando i tre vettori in un punto A, il segmento orientato che rappresenta w si trova sul piano individuato dai segmenti orientati che rappresentano u e v.

La negazione della dipendenza lineare conduce alla indipendenza lineare.

Definizione 3
Diciamo che tre vettori geometrici u, v e w sono linearmente indipendenti se la sola loro combinazione lineare nulla è quella banale.

Ciò significa che u, v e w sono linearmente indipendenti se e solo se

E' chiaro che, se w è linearmente dipendente da u e v allora i vettori u, v e w non sono linearmente indipendenti, perché, in questo caso, w = au + bv e quindi

Come nel caso di due vettori, anche in questa situazione, si vede facilmente che, viceversa, se i vettori u, v e w non sono linearmente indipendenti, cioé se esiste una loro combinazione lineare nulla e non banale, allora uno dei tre vettori è linearmente dipendente dagli altri due. Se infatti

è la combinazione lineare nulla e non banale e se c è il coefficiente non nullo, possiamo, dall'equazione precedente, ricavare w in funzione di u e v. Con calcoli analoghi a quelli precedenti troviamo

e quindi w risulta linearmente dipendente da u e v. Queste semplici osservazioni ci permettono di dare, come nel caso di due vettori, una caratterizzazione geometrica dell'indipendenza lineare di tre vettori geometrici.

• Tre vettori geometrici u, v e w sono linearmente indipendenti se e solo se, applicati in un punto A, danno luogo a tre segmenti orientati che non stanno sullo stesso piano.

Vediamo ora, dati tre vettori linearmente indipendenti u, v e w quali vettori geometrici troviamo combinando linearmente questi tre. Questo ci permetterà di vedere se esistono ulteriori vettori indipendenti da questi o se invece il processo finisce.
Supponiamo che il vettore geometrico z sia una combinazione lineare di u, v e w

e applichiamo i tre vettori a uno stesso punto A: u = AB, v = AC, w = AD. Non è difficile calcolare au, bv, cw e poi sommare i cammini. Sia au = AP, bv = AQ, cw = AR

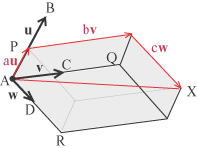Il risultato è un punto dello spazio, cosa poco interessante, mentre interessante è il fatto che ogni punto dello spazio X da luogo a un vettore geometrico AX che è combinazione linare di u, v e w. Sia infatti X un qualunque punto dello spazio euclideo, costruiamo la retta passate per X e parallela alla retta AD. Tale retta è complanare con AD e il loro piano interseca il piano ABC in una retta (postulato III della geometria dello spazio) la quale non può essere parallela ad AD perché w è linearmente indipendente da u e v.

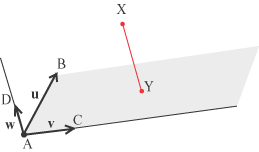Sia dunque Y il punto in cui la retta passate per X e parallela alla retta AD incontra il piano A, B, C definito dai vettori u, v. Costruiamo ora la retta passante per Y parallela alla retta AC

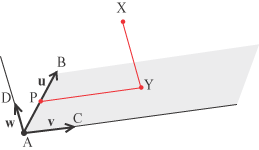e sia P il punto in cui questa retta incontra la retta AB. Abbiamo, sommando i cammini

Ma AP avendo la stessa direzione di u è un suo multiplo, PY avendo la stessa direzione di v è un suo multiplo, e YX avendo la stessa direzione di w è un suo multiplo, dunque qualunque sia X il vettore AX si può scrivere come combinazione lineare di tre vettori indipendenti. Notiamo che le parallele che ci servono esistono e sono uniche sempre in virtù del V postulato di Euclide, inoltre è il postulato III della geometria dello spazio tridimensionale che ci permette di affermare che il punto Y esiste: nel piano due rette non parallele si incontrano sempre, ma in tre dimensioni possiamo avere rette sghembe, rette cioè non parallele che non si incontrano, analogamente nello spazio a tre dimensioni due piani non paralleli si incontrano in una retta, ma con una dimensione in più si può immaginare che possano esistere "piani sghembi" piani cioè non paralleli che si incontrino in un solo punto. È proprio questo ciò che accade in uno spazio a quattro dimensioni ed è proprio questo ciò che esclude il postulato III quello, dunque, che fissa a tre le dimensioni dello spazio.
La conclusione di questi ragionamenti è che nello spazio euclideo si possono trovare uno, due, tre vettori linearmente indipendenti, ma non è possibile trovarne quattro!



Esercizi