e diciamo che x₁ è la prima componente di u, x₂ la seconda componente e x_n l'ennesima componente di u.
Due vettori numerici con lo stesso numero n di componenti possono sommarsi, componente per componente, dando luogo a un nuovo vettore numerico a n componenti. Se u = (x₁,x₂, ... ,x_n), e v = (y₁,y₂, ... ,y_n) allora definiamo

Questo operazione di somma ha tutte le proprietà formali che ha la somma tra vettori geometrici. In particolare esiste un vettore numerico nullo che indichiamo con 0 =(0,0,...,0) e un opposto : se u = (x₁,x₂, ... ,x_n) allora il suo opposto, che indichiamo con -u è dato da

e ovviamente u +(-u) = 0.
Seguendo l'analogia con i vettori geometrici possiamo introdurre anche l'idea di multiplo di un vettore. Se a è un numero reale e se u è un vettore numerico a n componenti allora il prodotto di a per u è un nuovo vettore numerico a n componenti definito dalla relazione

In definitiva l'insieme di tutti i vettori numerici a n componenti, insieme che si denota con Rⁿ, è chiuso rispetto alla operazione di somma e di prodotto di un vettore numerico per un numero, esattamente come accade per i vettori geometrici. Possiamo quindi, anche in questo contesto, considerare combinazioni lineari di vettori numerici e introdurre la fondamentale nozione di dipendenza e indipendenza lineare.

Un vettore numerico u è linearmente indipendente se è non nullo.
Osserviamo che, anche per i vettori numerici vale la legge di annullamento del prodotto:

Infatti se u= (x₁,x₂, ... ,x_n), allora a(x₁,x₂, ... ,x_n) = 0 se e solo se ax₁ = 0, ax₂ = 0 , ... , ax_n = 0 e quindi o a=0 oppure se a non è zero dovrà essere x₁ = 0, x₂ = 0, ... , x_n = 0 e quindi u=0.

La definizione 1 si può riformulare dicendo che u è linearmente indipendente e se e solo se au = 0 implica a = 0.

Definizione 2
Diciamo che due ¹ vettori geometrici u e v sono linearmente indipendenti se la sola loro combinazione lineare nulla è quella banale².
Ciò significa che u e v sono linearmente indipendenti se e solo se

viceversa, due vettori numerici u e v che non sono linearmente indipendenti, si dicono linearmente dipendenti. Ciò significa che esiste una loro combinazione lineare nulla non banale. Se au + bv = 0 è tale combinazione lineare e se a non è zero allora possiamo ricavare u dalla relazione precedente dividendo per a:

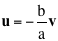
e dunque uno dei due vettori è multiplo dell'altro. Risulta quindi molto semplice verificare se due vettori sono o non sono linearmente dipendenti: basta verificare se uno è o meno multiplo dell'altro.
La situazione diventa complicata nel caso di tre o più vettori. Non tanto nella definizione che è una semplice estensione dei casi precedenti, quanto nel modo di stabilire se i vettori verificano o meno la condizione di indipendenza lineare.

Definizione 3
Diciamo che k vettori numerici a n componenti u₁, u₂,..., u_k sono linearmente indipendenti se e solo se la loro sola combinazione lineare nulla è quella banale.
Ciò significa che

La negazione della indipendenza lineare conduce alla dipendenza lineare: k vettori numerici sono linearmente dipendenti se esiste una loro combinazione lineare nulla non banale, se esistono cioè k numeri a₁, a₂, ... , a_k non tutti nulli tali che a₁u₁+a₂u₂ +...+a_ku_k = 0.

Nello spazio Rⁿ dei vettori numerici a n componenti possiamo trovare n vettori numerici linearmente indipendenti. Consideriamo le seguenti n-uple ordinate: e₁ = (1,0, ... ,0), e₂ = (0,1, ... ,0 ), ... , e_n = (0,0, ... ,1) dove il vettore e_i (i=1,2,...,n) ha tutte le componenti nulle tranne la i-esima che vale 1. Tali vettori sono linearmente indipendenti infatti se a₁e₁+a₂e₂ +...+a_ne_n = 0, allora, esplicitando il calcolo abbiamo:

e quindi a₁=0, a₂=0, ... , a_n=0. In definitiva la sola combinazione lineare nulla dei vettori e₁, e₂, ... , e_n è quella che ha tutti i coefficienti nulli.

Esercizi