Dimostrazione della disuguaglianza di Schwartz

Disuguaglianza di Schwartz
Dati due vettori numerici a n componenti u = (u₁,u₂, ... ,u_n) e v = (v₁, v₂ , ... ,v_n), risulta

dove l'uguaglianza vale se e solo se u e v sono linearmente dipendenti.

Consideriamo, al variare del numero reale x, il vettore numerico xu + v. Sia
M(x) = (xu + v).(xu + v) M(x) è una funzione positiva o nulla, ed è nulla se e solo se il vettore xu + v è nullo cioè se e solo se u e v sono linearmente dipendenti (vedi formula (7)). Dunque se u e v sono linearmente indipendenti la funzione M(x) è positiva per ogni valore di x. Sviluppiamo ora il "quadrato" di tale vettore usando le formule (3). (4), (5): abbiamo
M(x) = (xu + v).(xu + v) = (xu).(xu + v) + v.(xu + v) =
= (xu).(xu) + (xu).v + v.(xu) + v.v =
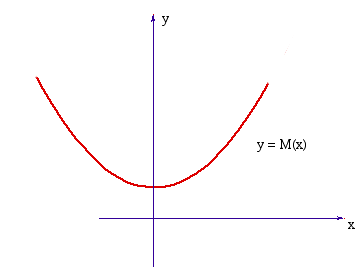
= x²u.u + 2x u.v + v.v Il grafico di questa funzione è una parabola con la concavità rivolta verso l'alto che non incontra l'asse delle x dal momento che M(x) > 0 per ogni x. Ne segue che l'equazione di secondo grado M(x) = 0 non ha radici reali e quindi il suo discriminante deve essere negativo cioè



D = (u.v)² - (u.u) (v.v) < 0 Tenendo conto che u.u = |u|² e v.v = |v|², la disuguaglianza (u.v)²< |u|²|v|², diventa, estraendo le radici quadrate,
|u.v|< |u||v|
Si osservi il diverso significato del simbolo di modulo: a sinistra |u.v| significa il modulo del numero reale u.v, mentre |u| significa il modulo del vettore numerico u. Analogamnte per |v|.