tali che la differenza di due termini successivi è una costante q detta ragione della progressione.

Ad esempio la successione

è una progressione aritmetica di ragione q = 4.
Se abbiamo due progressioni aritmetiche x = {x₁, x₂, x₃, ... } e y = {y₁, y₂, y₃, ... } possiamo costruire una nuova progressione

che risulta ancora una progressione aritmetica. Se infatti x ha ragione p e y ha ragione q allora la progressione z risulta una progressione aritmetica di ragione p+q dal momento che per ogni n >1

La progressione z così ottenuta sarà detta la somma della progressione x con la progressione y e si scriverà

Possiamo anche, in modo naturale, moltiplicare una progressione aritmetica per uno scalare a:

ottenendo, come si vede immediatamente, se q è la ragione di x, una progressione aritmetica di ragione aq.
Le due operazioni che abbiamo definite nell'insieme delle progressioni aritmetiche si comportano esattamente come le analoghe operazioni tra i vettori geometrici e tra i vettori numerici a n componenti. Abbiamo, anche in questa situazione, la progressione nulla

la progressione -x = {-x₁, -x₂, -x₃, ... } e possiamo calcolare combinazioni lineari e parlare di progressioni aritmetiche linearmente dipendenti e linearmente indipendenti. Ad esempio le due progressioni a = {2,5,8,11,14, ...} e b = {-4,-10,-16,-28,...} sono linearmente dipendenti dal momento che

Le progressioni

sono linearmente indipendenti. Se infatti fosse ae₁ + be₂ = 0, avremmo, uguagliando i primi due termini della successione, a=0 e a+b=0 cioè a=0 e b=0.
Possiamo anche verificare che le due progressioni e₁ ed e₂ e le loro combinazioni lineari generano tutte le possibili progressioni aritmetiche. Se infatti x è una qualunque progressione aritmetica allora abbiamo sempre

dove a è il primo termine della successione x e q è la sua ragione. Questa circostanza si esprime dicendo che le due progressioni {e₁ , e₂} formano una base per lo spazio delle progressioni aritmetiche. Questo fatto permette di descrivere in modo molto semplice le infinite progressioni aritmetiche "dosando", come si fa coi colori a partire da due colori base, i coefficienti della combinazione lineare: ad esempio una progressione di ragione 12 che inizia dal numero -4 si scriverà semplicemente come

VI 2. I quadrati magici

Una antica leggenda cinese fa risalire in tempi molto lontani la nascita dei quadrati magici: diagrammi numerici che per le loro straordinarie proprietà di simmetria facevano pensare a oggetti sopranaturali. La leggenda, che risale almeno al quinto secolo avanti Cristo, racconta che l'imperatore e ingegnere cinese Yu il grande fu aiutato a governare da due animali sopranaturali emersi dalle acque dei fiumi che solo lui aveva saputo controllare. Il primo animale fu un cavallo-drago nato dalle acque del Fiume Giallo che gli regalò il Ho Thu (il diagramma del Fiume) scritto in caratteri verdi, mentre il secondo, uscito dal Fiume Lo, era una tartaruga che gli regalò il Lo Shu (il diagramma del fiume Lo) scritto in rosso. Questi diagrammi si ritrovano nei libri di divinazione I Ching arrivati fino a noi. In particolare il Lo Shu assume la forma

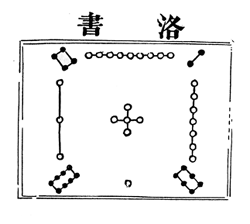che corrisponde al diagramma

dove se sommiamo i numeri sulle righe, sulle colonne o sulle diagonali troviamo sempre il numero 15.
In generale un quadrato magico 3x3 è un diagramma contenente 9 numeri disposti su tre righe (e tre colonne) in modo che la somma dei numeri su ogni riga, ogni colonna e ogni diagonale sia costante. Come le progressioni, anche i quadrati magici possono sommarsi tra loro sommando i termini che occupano lo stesso posto: il risultato di questa operazione conduce ancora, come è facile verificare, ad un nuovo quadrato magico. Possiamo anche definire, in modo naturale, il prodotto di un quadrato magico per uno scalare a: tale prodotto si otterrà moltiplicando ogni elemento per il numero a. Ancora il risultato di questa operazione è ancora un quadrato magico. Queste due operazioni ci permettono, a partire da qualche esempio di costruire infiniti altri quadrati magici. Partendo da quello cinese, e moltiplicandolo per 2 troviamo un nuovo quadrato magico

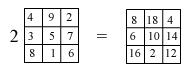Infiniti altri possono essere costruiti moltiplicando il quadrato cinese per un qualunque numero a. Ci domandiamo ora se, in questo modo, abbiamo esaurito tutti i possibili quadrati magici o ve ne sono degli altri. Ci domandiamo cioé se esiste un nuovo quadrato magico che non sia un multiplo di quello cinese, un quadrato magico dunque linearmente indipendente da quello. Uno molto semplice viene subito in mente: è quello che ha 1 in tutti i posti. Chiamiamo c il quadrato magico cinese e b quello con tutti 1. A partire da questi possiamo ora costruire altri, tanti altri quadrati magici: ad esempio se calcoliamo il quadrato 2b - c, troviamo un quadrato magico a somma 27.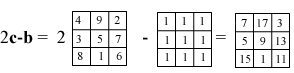

Abbiamo in questo modo trovato un criterio per costruire tutti i possibili quadrati magici o ve ne sono altri che non possono esprimersi a partire da b e c? In altre parole, esiste un quadrato magico linearmente indipendente da b e c? Permutando la prima e la terza colonna di c troviamo, ovviamente, un altro quadrato magico diciamo a. Se a fosse combinazione lineare di c e b sarebbe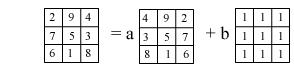

Ma questo è impossibile perché, uguagliando i tre termini della prima riga, si troverebbe il sistema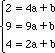

che è chiaramente incompatibile. Ne segue che a è linearmente indipendente da c e b. Possiamo a questo punto costruire infinito a tre (come si diceva nell'800) quadrati magici combinando linearmente i tre trovati. Si può dimostrare, ma non è immediato, che non esistono altri quadrati magici indipendenti da questi e quindi ogni quadrato magico 3x3 si può scrivere nella forma

Un altro modo per costruire facilmente dei quadrati magici indipendenti, si basa sulla seguente osservazione: se S è la somma (costante) degli elementi sulle righe, sulle colonne e sulle diagonali, allora l'elemento al centro del quadrato vale S/3. Infatti, se chiamiamo x tale elemento abbiamo che la somma degli elementi sulle due diagonali e di quelli sulla seconda riga vale 3S, d'altra parte questa somma si ottiene sommano la prima e la terza colonna e tre volte x. In definitiva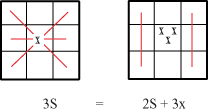

3x=S.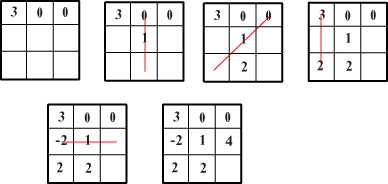
Tenendo conto di questo fatto, possiamo costruire un quadrato magico a partire, ad esempio, dai 3 elementi della prima riga: la somma di questi numeri mi dà l'elemento centrale e, a partire da questo, posso costruire gli altri. Vediamo come costruire quadrati con S=3

Osserviamo che l'ultimo numero da sistemare, che è -1, sistema, come una chiave di volta, sia la diagonale che la terza riga e la terza colonna. Questo fatto, se vogliamo sorprendente, ci permette di costruire facilmente altri due quadrati magici indipendenti da quello, spostando la posizione del 3 al secondo posto e al terzo posto. In definitiva otteniamo i tre quadrati magici linearmente indipendenti.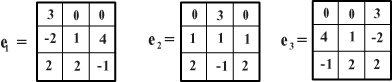

La loro indipendenza lineare si vede facilmente perché se fosse

i tre numeri sulla prima riga sarebbero 3x₁, 3x₂, 3x₃ e questi, essendo la prima riga del quadrato nullo, dovrebbero essere zero il che implica x₁ = 0, x₂ = 0, x₃ = 0. Possiamo anche, considerando sempre la prima riga, scrivere facilmente il quadrato cinese c come loro combinazione lineare:

Abbiamo trovato tre quadrati magici linearmente indipendenti e ci domandiamo, come abbiamo fatto per i vettori geometrici, se è possibile trovare un quarto quadrato magico indipendente da quelli. Anche in questo caso la risposta è negativa perché ogni quadrato magico lo possiamo scrivere come loro combinazione lineare. Consideriamo infatti un generico quadrato magico x e supponiamo che 3x₁, 3x₂, 3x₃, siano i numeri che si trovano sulla sua prima riga, cosa questa non restrittiva dato che possiamo dividere per tre i numeri effettivi che si trovano in queste caselle. Costruiamo ora il quadrato magico

e dimostriamo che x' = x. Per dimostrare che due quadrati magici sono uguali basterà dimostrare che hanno gli stessi 9 numeri nelle stesse posizioni. Il quadrato x' sulla prima riga ha i numeri 3x₁, 3x₂, 3x₃ come x e inoltre avendo uguale la prima riga, la somma S = 3x₁ + 3x₂ + 3x₃ sarà la stessa per i due quadrati magici. Ne segue, per la proprietà generale dei quadrati magici che abbiamo visto sopra, che il termine centrale vale S/3 per tutti e due i quadrati magici. A questo punto possiamo concludere che i due quadrati magici sono uguali dato che gli altri termini sono univocamente individuati dalla condizione che la somma sulle due diagonali, sulle righe e sulle colonne vale S per entramnbi. Ad esempio l'elemento centrale dell'ultima riga sarà per entrambi la soluzione y dell'equazione

Esiste anche un celebre quadrato magico 4x4 raffigurato in un quadro (melamconia) di Durer un pittore tedesco rinascimentale.

Sotto la campana è scolpito sul muro il quadrato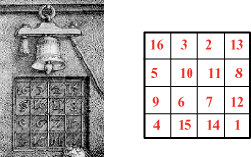

In questo caso la somma dei numeri sulle righe le colonne e le diagonali fa sempre 34. I numeri 15, 14 sull'ultima riga indicano la data nella quale è stato realizzato il quadro : 1514.
La situazione nel caso di quadrati magici 4x4 è, dal punto di vista del calcolo, molto più complicata, mentre dal punto di vista concettuale la situazione risulta del tutto analoga. Questi oggetti possono sommarsi e moltiplicarsi per uno scalare riproducendosi tra loro. La loro totalità costituisce uno spazio vettoriale che può essere studiato con algoritmi generali che permettono di individuare il numero minimo di vettori coi quali descrivere ogni altro vettore come loro combinazione lineare. Più avanti svilupperemo un metodo generale che premette di calcolare questi generatori.