|
VII 1. La nozione di spazio vettoriale su un campo K
Sia K un campo, cioè un insieme di elementi tra i quali sono definite le 4 operazioni elementari dell'aritmetica: somma,
differenza, prodotto
e divisione con le stesse proprietà formali che valgono per gli ordinari insiemi di numeri. Una definizione dettagliata
di questa struttura e delle sue proprietà sarà data nel corso di Algebra. In questo corso, per semplicità,
supponiamo, salvo avviso contrario, che K sia l'insieme dei numeri reali. Gli elementi di K saranno anche detti anche, seguendo una terminologia
usata soprattutto dai fisici, scalari e saranno indicati con caratteri corsivi.
Uno spazio vettoriale V sul campo K è dato da un insieme V, i cui elementi sono detti vettori, sulla natura
concreta dei quali nulla è noto, ma che è possibile far interagire tra loro e con gli scalari rispettando alcune regole
formali che ci consentono di fare calcoli algebrici analoghi a quelli che si eseguono nell'aritmetica elementare. I vettori
saranno sempre indicati con lettere in grassetto.
Le regole che postuliamo sono le seguenti.
Dati due elementi di V, u e v, è possibile determinare in modo univoco un ben definito ulteriore elemento di V,
che dipende da quelli, che denotiamo con u + v e che chiamiamo la somma di u con v.
Postuliamo che questa operazione di somma verifichi le seguenti proprietà
- (u + v) + w = u + (v + w) (proprietà associativa)
comunque si scelgano i tre elementi u, v e w in V
- u + v = v + u
(proprietà commutativa)
comunque si scelgano i due elementi u, v in V
- Esiste un ben determinato elemento di V, che denotiamo col simbolo 0, tale che, per ogni vettore u di V risulti
0 + u = u
(esistenza del vettore nullo)
- Per ogni vettore u di V esiste un ben definito vettore che chiamiamo opposto di u e indichiamo
col simbolo -u , tale che
u + (-u ) = 0
(esistenza dell'opposto)
Per semplificare la notazione, come normalmente viene fatto nell'aritmetica elementare, indichiamo il vettore u+(-v)
col simbolo u - v, vettore questo che viene anche detto differenza di u con v.
Oltre a questo, postuliamo che sia definita una ulteriore operazione che permette di moltiplicare uno scalare a
di K con un vettore
u di V ottenendo come risultato un nuovo vettore denotato col simbolo a.u. Postuliamo che questa ulteriore
operazione verifichi
le seguenti proprietà, per ogni possibile scelta degli scalari a e b e dei vettori u e v:
- (a + b).u = a.u + b.u
- a.(u + v) = a.u + a.v
- a.(b.u) = (ab).u
- 1.u = u e (-1).u= -u
A partire da queste regole di calcolo che postuliamo e usando quelle che Euclide chiama nozioni comuni possiamo costruire una
teoria matematica assiomatico-deduttiva fatta di definizioni, teoremi e dimostrazioni. Le nozioni comuni che permettono di articolare delle
dimostrazioni formalmente corrette stabiliscono che:
- se a cose uguali aggiungiamo (o togliamo) cose uguali ciò che resta sono cose uguali
In simboli: se A = B allora A + C = B + C
- se moltiplichiamo (o dividiamo) cose uguali per cose uguali, ciò che resta sono cose uguali
In simboli: se A = B allora a.A = a.B
Alcune proprietà utili nel calcolo si dimostrano facilmente a partire dagli assiomi e dalle nozioni comuni. Diamo di seguito
alcune di queste utili nei calcoli vettoriali.
- 0.u = 0 per ogni vettore u dello spazio ( regola di annullamento del prodotto)
(dimostrazione)
- -(-u) = u per ogni vettore u dello spazio ( regola dei segni)
(dimostrazione)
- a(u1 + u2 + ... + un) =
au1 + au2 + ... + aun
(dimostrazione)
- (a1 + a2 + ... + an) .u =
a1 .u+ a2.u + ... + an.u
(dimostrazione)
Se V è uno spazio vettoriale e se W è un sottoinsieme non vuoto di V
i vettori di W possono sommarsi e moltiplicarsi per uno scalare,
essendo in particolare dei vettori di V. Quando accade che, operando in tutti i modi possibili con queste due operazioni,
coi vettori di W si trova sempre un vettore di W, diciamo che W è un sottospazio vettoriale di V. In altri termini
W è un sottospazio vettoriale di V se e solo se è non vuoto e
- la somma di due qualunque vettori di W è un vettore di W
- il prodotto di un qualunque scalare a per un qualunque vettore w di W è ancora un vettore di W.
I primi esempi di sottospazi vettoriali vengono dalla geometria. Sia V lo spazio vettoriale formato dai vettori geometrici e sia
r una retta dello spazio. L'insieme dei vettori geometrici AB definiti da due punti A e B delle retta r si chiama
la direzione di r, spazio che indichiamo col simbolo Wr:
Wr = {AB : A 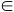 r, B r, B 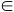 r} r}
Analogamente, se  è un piano dello spazio, l'insieme dei vettori geometrici AB definiti
da due punti A e B del piano è un piano dello spazio, l'insieme dei vettori geometrici AB definiti
da due punti A e B del piano  si chiama
la gicitura si chiama
la gicitura  , spazio che indichiamo col simbolo
W , spazio che indichiamo col simbolo
W : :
W = {AB : A = {AB : A 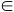
 , B , B 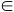  } }
E' chiaro che questi sottoinsiemi di V sono sottospazi vettoriali. Indichiamo la dimostrazione nel caso dei piani.
Siano AB e CD due vettori di
W allora la somma AB + CD è ancora un vettore di
W allora la somma AB + CD è ancora un vettore di
W , infatti possiamo intanto trovare un punto D' del piano , infatti possiamo intanto trovare un punto D' del piano  tale che
CD = BD' e quindi il vettore AB + CD = AB + BD' è un vettore di
W
tale che
CD = BD' e quindi il vettore AB + CD = AB + BD' è un vettore di
W . Ugualmente è facile vedere che se AB è un vettore di
W . Ugualmente è facile vedere che se AB è un vettore di
W allora ogni suo multiplo è un vettore di W allora ogni suo multiplo è un vettore di W .
Infatti il vettore aAB = AC individua un punto C della retta AB, la quale, essendo A e B punti di .
Infatti il vettore aAB = AC individua un punto C della retta AB, la quale, essendo A e B punti di
 è contenuta in è contenuta in  . Ne segue che anche il punto C è contenuto in . Ne segue che anche il punto C è contenuto in  e quindi AC è un vettore di W e quindi AC è un vettore di W . .
L'introduzione di questi spazi è molto importante perché permette di tradurre fatti geometrici nel linguaggio
degli spazi vettoriali. Ad esempio se r e r' sono due rette dello spazio, allora r è parallela a
r' se e solo se Wr = Wr'.
Analogamente se  e e
 ' sono due piani dello spazio allora ' sono due piani dello spazio allora  e e  '
sono paralleli se e solo se W '
sono paralleli se e solo se W = W = W '. '.
Sia V uno spazio vettoriale diciamo che un vettore u è
combinazione lineare dei vettori u1, u2, ... , um
se esistono degli scalari a1, a2, ... ,am tali che
u = a1.u1 + a2.u2 +... +
am.um
Fissati i vettori u1, u2, ... , um, l'insieme di tutte le
loro possibili combinazioni lineari è un sottoinsieme di V che viene chiamato lo spazio generato dai vettori u1, u2, ... , um e che si indica col simbolo
Span(u1, u2,
... , um). In formule
Span(u1, u2,
... , um) = { a1u1 + a2u2 + ... +
amum | al variare degli scalari a1, a2,
... ,am}
Teorema VII 1
Dati m vettori, u1, u2, ... , um, di uno spazio vettoriale V,
il sottoinsieme
Span(u1, u2, ... , um) è un sottospazio vettoriale di V.
(dimostrazione)
Un problema che si pone è quello di sapere quando, dati due insiemi di vettori, uno formato dagli m vettori u1, u2,
... , um e l'altro dai k vettori v1, v2, ... , vk, risulti
Span(u1, u2, ... , um) =
Span(v1, v2, ... , vk)
Il problema è interessante anche quando si tratti di pochi vettori. Già nel caso m=1, n=1 non è del tutto ovvio
un criterio che mi dica quando Span(u) = Span(v). Discutiamo nella
nota alcuni criteri proposti dagli
studenti utili a chiarire il ruolo e l'importanza dei quantificatori (per ogni ed esiste) nella matematica moderna.
Il seguente teorema ci offre un criterio molto semplice per rispondere alla nostra domanda
Teorema VII 2
Dati due insiemi finiti di vettori di uno spazio vettoriale V, uno formato dagli m vettori u1, u2,
... , um e l'altro dai k vettori v1, v2, ... ,
vk, risulta
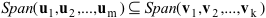
se e solo se
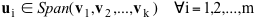 (dimostrazione)
(dimostrazione)
Dal teorema 2 segue che
Span(u1, u2, ... , um) =
Span(v1, v2, ... , vk)
se e solo se tutti gli m vettori ui (i=1,2,...,m) appartengono allo spazio Span(v1, v2, ... , vk), cosí che, per il teorema 2, lo spazio generato dai vettori u risulta contenuto nello spazio generato dai vettori v, e in più tutti i vettori vj (j=1,2,...,k) appartengono allo spazio Span(u1, u2, ... , um) , cosí che, per il teorema 2, lo spazio generato dai vettori v risulta contenuto nello spazio generato dai vettori u. I due spazi risultano quindi uno incluso nell'altro e pertanto sono uguali.
Il teorema precedente implica anche che, se il vettore um è combinazione lineare dei vettori
u1, u2, ... , um-1, allora
Span(u1, u2, ... , um) =
Span(u1, u2, ... , um-1)
Esercizi
| |
