dove d_i,j è il simbolo di Kronecker che vale 1 se i = j, zero altrimenti.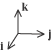
Una base di V formata da un insieme di vettori ortonormale, si chiama una base ortonormale di V.

La base, usata spesso dai fisici, {i, j, k} dello spazio dei vettori geometrici è una base ortonormale: i e j sono due direzioni orizzontali ortogonali tra loro (normalmente i diretto a est e j a nord) mentre k è orientato verticalmente verso lo zenit. I vettori risultano così ortogonali a due a due e sono poi presi di modulo 1 (cosa che si può esprimere dicendo con un linguaggio sopratutto fisico, che sono dei versori).

Notiamo che questa base ortonormale è definita solo a partire dalla posizione di un uomo in un dato punto dello spazio poichè solo rispetto a questo le parole orizzontale verticale hanno un significato.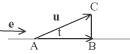

In Rⁿ invece abbiamo una base che si impone immediatamente all'attenzione che è la base canonica, quella formata dai vettori (1,0,0,...,0), (0,1,0,...,0), (0,0,1,..,0), ... , (0,0,0,...,1). Si vede facilmente, per come è definito il prodotto scalare in Rⁿ, che questi vettori sono a due a due ortogonali e sono tutti di modulo 1. La base canonica è dunque una (non la sola ovviamente) base ortonormale Rⁿ.

Le basi ortonormali sono molto utili nello studio degli spazi vettoriali. Ad esempio se {e₁,e₂,...,e_n} è una base ortonormale di V allora le componenti di un qualunque vettore u, in quella base, sono le sue proiezioni ortogonali sui vettori e_i. Ricordiamo che, nel contesto dei vettori geometrici, se e è un vettore di modulo 1 allora la proiezione ortogonale di un vettore u lungo la direzione e

è il vettore AB = (u.e)e, infatti il segmento AB ha come lunghezza |u|cos(t) e poichè e è di modulo 1 tale numero coincide con |e||u|cos(t) = u.e. Ne segue che i vettori AB e (u.e)e sono uguali perché hanno la stessa direzione lo stesso verso (quello di e) e lo stesso modulo.
La situazione geometrica ci permette, usando i nostri postulati, di definire in astratto, nel contesto di uno spazio vettoriale qualunque, la proiezione ortogonale di un vettore u sul versore e: tale proiezione è il vettore (u.e)e.
In generale se:

le componenti a_i della combinazione lineare coincidono con le proiezioni ortogonali di u sul versore e_i. Abbiamo infatti, moltiplicando scalarmente per e_i:

si vede facilmente che V ha dimensione minore di 4 essendo un sottospazio proprio di R⁴, inoltre i 3 vettori di V

sono linearmente indipendenti e dunque V è di dimensione 3 e questi tre vettori sono una sua base. Tuttavia questi vettori non sono ortogonali tra loro. Ad esempio u₁ non è ortogonale a u₂ dato che u₁.u₂ = -1. Anche dal punto di vista dei moduli questi vettori non vanno bene dato che hanno tutti come modulo la radice di 2.

L'algoritmo di Gram-Schmidt, che ora esponiamo, da un procedimento per ricavare da un qualunque insieme di generatori di un dato spazio vettoriale, una base ortonormale. Sia

• Se u₁ = 0 eliminiamolo dal nostro elenco. Sarà ancora Span(u₁, u₂, ... , u_m) = Span(u₂, ... , u_m). Se invece u₁ non è zero sostituiamolo con il suo normalizzato cioè col vettore

  Il vettore e₁ ha modulo 1 e Span(u₁, u₂, ... , u_m) = Span(e₁, u₂, ... , u_m) dato che
  e₁ Span(u₁, u₂, ... , u_m) e u₁ Span(e₁, u₂, ... , u_m).
  Se i vettori della lista sono esauriti, l'algoritmo è finito: {e₁} è una base ortonormale di V e dim V = 1, altrimenti tra i generatori di V esiste un altro vettore u₂

• Togliamo da u₂ la sua proiezione ortogonale su e₁ in modo che il vettore restante e'₂ = u₂ - (u₂.e₁)e₁

  sia ortogonale a e₁. Se e'₂ = 0 allora u₂, essendo combinazione lineare di e₁, può essere tolto dalla lista e Span(e₁, u₂, u₃, ... , u_m) = Span(e₁, u₃, ... , u_m). Altrimenti sostituiamo u₂ con il normalizzato di e'₂ cioè con
  

  

  A questo punto e₁ e e₂ sono due vettori di modulo 1 e ortogonali tra loro. Inoltre

  V= Span(e₁, u₂, u₃, ... , u_m) = Span(e₁, e₂, u₃, ... , u_m)

  dato che e₂ Span(e₁, u₂, ... , u_m) e u₂ Span(e₁, e₂, ... , u_m).
  Se i vettori della lista sono esauriti, l'algoritmo è finito:{e₁,e₂} è una base ortonormale di V e dimV = 2, altrimenti tra i generatori di V esiste un altro vettore u₃ e possiamo iterare il procedimento.

• Togliamo da u₃ la sua proiezione ortogonale sullo spazio generato da e₁ e e₂ in modo che il vettore restante e'₃ = u₃ - [(u₃.e₁)e₁ + (u₃.e₂)e₂]

  sia ortogonale sia a e₁ che a e₂ ¹ . Se e'₃ = 0 allora u₃, essendo combinazione lineare di e₁ ed e₂ , può essere tolto dalla lista e Span(e₁, e₂, u₃ ... , u_m) = Span(e₁, e₂, ... , u_m). Altrimenti sostituiamo u₃ con il normalizzato di e'₃ cioè con
  

  

  A questo punto e₁ , e₂ , e₃ sono tre vettori di modulo 1 e ortogonali tra loro a due a due. Inoltre

  V= Span(e₁, e₂, u₃, ... , u_m)= Span(e₁, e₂, e₃, ... , u_m)

  dato che e₃ Span(e₁, e₂, u₃, ... , u_m) e u₃ Span(e₁, e₂, e₃, ... , u_m)
  Se i vettori della lista sono esauriti, l'algoritmo è finito: {e₁,e₂,e₃} è una base ortonormale di V e dim V = 3, altrimenti iteriamo il procedimento col vettore successivo fino ad esaurimento dei vettori.

dove

e applichiamo l'algoritmo di Gram-Schmidt a questi tre vettori.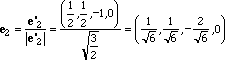

Si vede immediatamente che i tre vettori {e₁,e₂,e₃} sono vettori di V dal momento che la somma delle loro componenti è zero e inoltre sono di modulo 1 e a due a due ortogonali.
E' interessante osservare che se si applica l'algoritmo ordinando diversamente i tre vettori il risultato cambia e il calcolo diventa anche più semplice. Applichiamo l'algoritmo ai vettori

Il calcolo viene più semplice perché ora il secondo vettore è già ortogonale al primo e quindi la proiezione ortogonale del secondo vettore sul primo è nulla e basta normalizzarli dividendoli per il loro modulo. Il risultato finale produce la base