Lezioni di Geometria

Franco Ghione


Capitolo XIV



Equazioni di un piano nello spazio euclideo tridimensionale

Sia E3 l'insieme dei punti dello spazio euclideo di dimensione 3 e V l'insieme dei suoi vettori geometrici. Un piano dello spazio è definito se conosciamo la sua giacitura W e un suo punto A. Infatti, in questo caso, i punti del piano sono tutti e soli i punti P di E3 per i quali il vettore AP appartiene a W. Se scegliamo una base di W, cioè due vettori linearmente indipendenti per i quali W = Span(u,v), questa condizione equivale all'esistenza di due scalari t ed s tali che

AP = t u + sv

Questa relazione vettoriale diventa una relazione analitica se introduciamo un sistema di coordinate cartesiane nello spazio E3. Fatto questo infatti A sarà individuato dalle sue coordinate:
A=(x1,y1,z1)
e i due vettori che generano la giacitura dalle loro componenti
u = u1i + u2j + u3k
v = v1i + v2j + v3k.
Se P =(x,y,z) è un punto generico dello spazio, relazione vettoriale precedente si scrive

(x - x1)i + (y - y1) j + (z - z1)k = t(u1i + u2j + u3k) + s(v1i + v2j + v3k) =
= (au1 + bv1)i + (au2 + bv2)j + (au3 + bv3)k

Poiché un vettore si scrive in modo unico come combinazione lineare di vettori di una base, da questa relazione troviamo le tre equazioni:


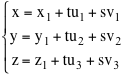(equazioni parametriche di un piano)



Queste equazioni, che si chiamano equazioni parametriche del piano passante per il punto A e di giacitura W = Span(u,v), possono essere scritte in modo più semplice e compatto usando i vettori (colonna) numerici a tre componenti con le loro regole di calcolo


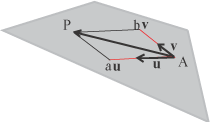
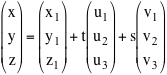Si deve però fare attenzione al diverso significato dei simboli: le prime due colonne rappresentano le coordinate dei punti P ed A nel sistema diriferimento (O,i,j,k), mentre le seconde due rappresentano le componenti dei vettori u e v nella base i,j,k.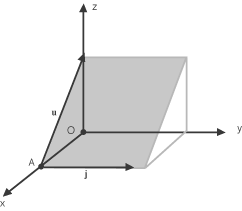
In definitiva le equazioni parametriche di un piano forniscono, in forma esplicita, le coordinate di un punto del piano in funzione di due parametri liberi t ed s. Per determinare queste equazioni si deve conoscere un punto A del piano e la sua giacitura W. Conoscere un punto A significa conoscere le sue coordinate mentre conoscere la giacitura W significa conoscere una base u,v di W. Ovviamente dato un piano, vi sono infinite scelte possibili sia per il punto A che per la base u,v di W. Scelte diverse danno ovviamente luogo a diverse equazioni dello stesso piano.

Esempio
Consideriamo il piano passante per il punto A = (1,0,0), parallelo al vettore j e inclinato di 45 gradi rispetto al piano orrizontale, come mostrato in figura.

Per scrivere le equazioni parametriche di questo piano dobbiamo trovare un suo punto (e questo può essere il punto A = (1,0,0) che già conosciamo) e due vettori indipendenti del piano che generano la sua giacitura. Questi possono essere u = -i + k e j e dunque la giacitura del piano sarà W=Span(-i + k, j). Fatte queste scelte, possiamo scrivere le equazioni parametriche del piano: queste si ottengono sostituendo i 9 valori noti (le tre coordinate di A e le sei componenti dei vettori u e v) nelle equazioni precedenti. Troviamo così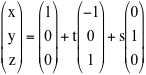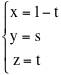

                    

Al variare dei due parametri t e s troviamo tutti e soli i punti del piano. Ad esempio il punto (1,1,1) non appartiene al piano perché non è possibile ottenerlo dalle equazioni precedenti, qualunque sia la scelta di s e t. Il punto T=(0,3,1) invece appartiene al piano perché si ottiene per t=1 e s=3. Osserviamo che i parametri t e s hanno un significato geometrico: essi permettono di trovare il vettore AT = u + 3j e quindi la posizione di T sul piano.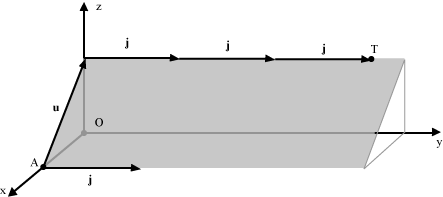



Equazione cartesiana di un piano
Esiste un secondo modo per descrivere analiticamente i punti di un piano che consiste nel presentare la sua giacitura W come lo spazio ortogonale a uno spazio Span(u) generato da un vettore non nullo w ortogonale al piano.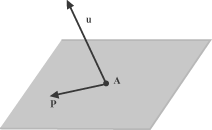
W = Span(u)
Se conosciamo u e un punto A del piano, un generico punto P appartiene a quel piano se e solo se il vettore AP è ortogonale al vettore u.

Fissato un sistema di coordinate, supponiamo che A abbia le coordinate A = (x1,y1,z1) e che u = ai + bj + ck. Un generico punto P = (x,y,z) definisce un vettore AP ortogonale ad u se e solo se

[(x - x1)i + (y - y1) j + (z - z1)k]. [ai + bj + ck] = 0

Cioé se e solo se ax + by + cz = ax1 + by1 + cz1. Se indichiamo con d la quantità nota ax1 + by1 + cz1 otteniamo la
ax + by + cz = d

(equazione cartesiana di un piano)



Le coordinate dei punti di un piano verificano dunque una equazione di primo grado in x,y,z. Viceversa i punti che verificano una equazione di primo grado si trovano su un piano: il piano perpendicolare al vettore u = ai + bj + ck passante per uno dei punti A = (x1,y1,z1) che verificano la data equazione. Ad esempio l'equazione 2x - y + z = 1 rappresenta un piano perpendicolare al vettore 2i - j + k passante per il punto (1,2,1): tale piano infatti, svolgendo il calcolo precedente, sarebbe proprio

2x - y + z = 2.1 -1.2 + 1.1 = 1.


Esempio
Scriviamo l'equazione cartesiana del piano che abbiamo considerato nell'esempio precedente. Dobbiamo prima di tutto trovare un vettore u perpendicolare al piano: un tale vettore è, ad esempio il vettore i + k che è ortogonale a -i + k e a j. Come punto possiamo ancora prendere il punto A = (1,0,0). L'equazione cartesiana del piano diventa allora

x + z = 1

I punti le cui coordinate verificano l'equazione sono punti del piano e, viceversa, quelli che non la verificano non sono punti del piano. Vediamo anche in questo modo che il punto (0,3,1) appartiene al piano mentre il punto (1,1,1) non appartiene al piano.

In definitiva l'equazione cartesiana del piano fornisce una caratteristica algebrica che deve essere soddisfatta dalle coordinate dei punti del piano. Per trovare questi punti occorre dunque risolvere l'equazione: ogni soluzione cioè ogni terna che verifica l'equazione dà le coordinate di un punto del piano. Per questo si dice che l'equazione cartesiana del piano definisce implicitamente i punti del piano, per averli esplicitamente si deve risolvere l'equazione. Questo passaggio, il risolvere l'equazione, corrisponde al passaggio dall'equazione cartesiana a quelle parametriche dove le coordinate dei punti del piano sono esplicitate. Nell'esempio precedente, per risolvere l'equazione x+z=1, possiamo dare a z un qualunque valore t, la x sarà allora x=1-z=1-t e la y, non comparendo nell'equazione può assumere un qualunque valore s. Le soluzioni dell'equazione sono dunque (1-t,s,t) dove i parametri t e s possono essere quello che vogliono, sono come si dice, parametri liberi.
Viceversa, per passare dalle equazioni parametriche a quella cartesiana, basta eliminare dalle tre equazioni parametriche i due parametri. Nell'esempio che abbiamo considerato, sostituendo il valore t=z, che si ricava dalla terza equazione, nella prima equazione troviamo x=1-z che è l'equazione cartesiana del piano in questione.

Esercizi