|
Lezioni di Geometria Franco Ghione |
 |
L'algoritmo di Gauss
L'algoritmo di Gauss
fornisce una semplice procedura di calcolo per trasformare un insieme di generatori di un dato spazio vettoriale U
in una base particolarmente semplice. Esso permette, una volta eseguito, di calcolare facilmente la dimensione di U e una base per lo spazio
U^ ortogonale a U. Applicato alla matrice dei coefficenti di un sistema omogeneo
di equazioni lineari l'algoritmo permette di ricavare una base per lo spazio delle soluzioni. Consideriamo ora un sistema finito u1, u2, ... , um
di vettori di V e sia U lo
spazio che loro generano, lo spazio cioè formato da tutte le loro possibili combinazioni lineari.
La dimensione dello spazio U sarà comunque minore del numero di generatori cioè dim U < m.
Infatti se questi generatori sono linearmente indipendenti essi formano una
base
di U e quindi la sua dimensione è m, ma se questi generatori sono tra
loro dipendenti, questa dimesione diventa strettamente minore di m. Quello che cerchiamo è allora
un algoritmo che trasformi i generatori u1, u2, ... , um di U in altri generatori
linearmente indipendenti e dentro lo spazio U. Questo algoritmo si basa su una così detta operazione elementare
il cui significato astratto è espresso dalla formula seguente:
Possiamo, in virtù di questa formula, sostituire un generatore v di U con un vettore ottenuto sommando a v
un multiplo scalare di un'altro generatore u,
senza alterare lo spazio U generato da tali vettori.
è un vettore di Span(u, au+v).
Applicando intelligentemente più volte questa operazione elementare,e cambiando eventualmente l'ordine dei vettori,
possiamo risolvere il problema che ci siamo posti.
Descriviamo ora dettagliatamente l'algoritmo. u2 = a21e1 + a22e2 + ... + a2nen . . . . . . . . . . . . . . . . . . . . . . . . . um = am1e1 + am2e2 + ... + amnen 2. Scriviamo le componenti dei vettori così ottenute come righe di una matrice 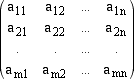 3. Scegliamo sulla prima colonna di questa matrice un elemento non nullo detto pivot. Se tale elemento non esiste
passiamo in rassegna la colonna successiva. Se tutte le colonne sono nulle l'algoritmo si ferma. Altrimenti
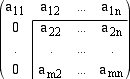 7. Ripetiamo i passi 3,4,5,6 sulla sottomatrice incorniciata e proseguiamo in questo modo fino all'esaurimento di tutte le colonne. Alla fine del processo la matrice ha la forma a scala e viene detta matrice ridotta.  Le k righe non nulle della matrice ridotta sono,
in quanto vettori numerici riga di Rn linearmente indipendenti, e tali sono anche i vettori v1,v2, ..., vk
di U ottenuti da quelle righe tramite la base B di V. Abbiamo allora
ma ora i vettori v sono linearmente indipendenti e poiché le operazioni elementari che abbiamo fatte per trovarli, non hanno cambiato lo spazio U,
essi sono anche un insieme di generatori e dunque sono una base per U che per questo risulta di dimensione k. 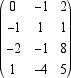 Prendiamo come pivot per la prima colonna il numero 1 e portiamo quindi la quarta riga al primo posto  eseguiamo le operazioni 5. e 6. sulla prima colonna per ottenere con operazioni elementari degli zeri: sommiamo la prima riga con la terza, e poi moltiplichiamo la prima riga per 2 e sommiamola alla quarta 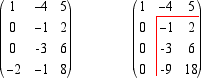 Prendiamo come pivot sulla seconda colonna -1. Eseguendo le operazioni elementari sulle ultime due righe otteniamo la matrice ridotta 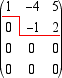 le prime due righe danno i vettori v1 = -i - 4j + 5k e
v2 = -j + 2k che sono evidentemente linearmente indipendenti e che, essendo ottenuti da
u1, u2, u3, u4 attraverso operazioni elementari generano lo spazio U.
Abbiamo dunque ed essendo v1, v2 linearmente indipendenti essi formano una base (ridotta) di U
e pertanto dim U = 2. 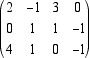 Riduciamo la matrice con l'algoritmo di Gauss: scegliamo come pivot per la prima colonna 2, moltiplichiamo la prima riga per -2 e sommiamola
alla terza; prendiamo 1 come pivot per la seconda colonna, moltiplichiamo la seconda riga per -3 e sommiamola alla terza. La sequenza di operazioni che
abbiamo detto portano alle matrici  L'ultima matrice è ridotta e i suoi tre pivot sono 2, 1, -9. I vettori v1 = (2,-1,3,0),
v2 = (0,1,1,-1) e v3 = (0,0,-9,2) sono chiaramente linearmente indipendenti e dunque dim U = 3 e dato che i tre vettori u1, u2, u3 generano uno spazio vettoriale di dimensione 3
questi vettori sono anch'essi linearmente indipendenti.
Corollario 4. (ii)
Si chiamo rango per righe di una matrice la dimensione dello spazio generato dalle righe. Nella teoria delle matrici questo numero, che è anche il massimo numero di righe linearmente indipendenti, è molto importante. L'algoritmo di Gauss permette anche di trattare un qualunque sistema di equazioni lineari omogeneo o non omogeneo e di stabilire se il sistema è oppure no compatibile. Questa estenzione si trova nel capitolo Rango di una matrice e sistemi lineari. Esercizi |