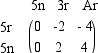La matrice può anche pensarsi, in questa semplicissima situazione, come uno schema per rappresentare in una immagine sintetica tutti i dati del problema e scegliere la strategia migliore. In questo caso è il giocatore R giocherà il 5 nero perché in quel modo, nel peggiore dei casi andrà pari, mentre il giocatore C giocherà il 5 nero per evitare perdite.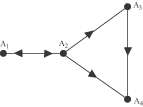

Reti di comunicazione
Supponiamo di avere n individui che chiamiamo A₁, A₂, ... ,A_n e supponiamo che esistano una serie di collegamenti tra gli individui della rete. Se esiste un collegamento da A_i ed A_j non è detto che esista anche un collegamento tra A_j ed A_i, quando invece tale collegamento esiste diciamo che il collegamento tra l'individuo A_i e l'individuo A_j è reciproco. Una rete di comunicazione può essere rappresentata tramite un grafo, una immagine bidimensionale che rappresenti tutti gli individui della rete e i loro collegamenti. Per ottenere tale grafo si rappresentano gli individui con dei punti e il collegamento tra l'individuo A_i e l'individuo A_j con una linea orientata che unisce A_i con A_j. La figura seguente rappresenta una rete di comunicazione tra 4 individui: il collegamento tra A₁ e A₂ è reciproco mentre gli altri non lo sono.

Una rete di comunicazione tra n individui può anche rappresentarsi con una matrice quadrata a n x n: l'elemento a_i,j di questa matrice vale 1 se esiste un collegamento tra A_i ed A_j, zero nel caso contrario. Questa matrice ha tutti zeri sulla diagonale principale e, quando tutti i collegamenti sono reciproci la matrice che si ottiene è una matrice simmetrica. Nel caso della rete descritta dalla figura precedente, otteniamo

In questo caso le potenze della matrice della reta ammettono una interessante interpretazione. Se A è la matrice di una data rete, allora A² rappresenta le possibili connessioni in due passaggi, A³ in 3 passaggi e così via. L'elemento a_h,k della matrice A² infatti è dato da

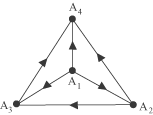la sua matrice è la matrice A data da: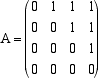

eseguento i quadrato di A otteniamo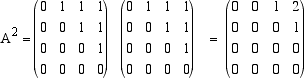

Notiamo che, guardando la matrice, esistono due collegamenti in due passi tra A₁ e A₄: il primo passa per A₂ e il secondo per A₃.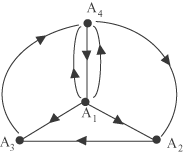



Esempio 2
Supponiamo che la rete seguente rappresenti le connessioni aeree tra 4 città:

La matrice che rappresenta la rete è la matrice A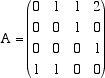

Il numero 2 al posto 1,4 sta a indicare che esistono due collegamenti tra A₁ e A₄.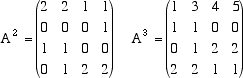
In generale, anche in questa situazione il prodotto A² rappresenta la rete di connessioni con due voli. Infatti, non tenendo conto delle coincidenze più convenienti, se esistono a_h,1 connessioni dirette tra la città A_h e A₁ e esistono a_1,k connessioni dirette tra A₁ e A_k, allora esistono a_h,1.a_1,k voli che collegano A_h e A_k facendo scalo a A₁ dal momento che, per ciscun volo con cui si va da A_h ad A₁ si può proseguire da A₁ a A_k con qualunque dei a_1,k voli disponibili. Facendo le potenze di A otteniamo quindi informazioni sui possibili collegamenti con uno o più scali.

Osserviamo che, con uno scalo, non tutte le città sono collegate (ad esempio da A₂ non è raggiungibile A₁) mentre con uno o due scali tutte le città risultano collegate tra loro dal momento che la matrice A + A² + A³ ha tutti i coefficienti non nulli.

Le matrici in ecologia
Il modello che presentiamo a titolo di esempio descrive la crescita (o l'estinzione) di una popolazione di scarabei. La popolazione viene intanto divisa in tre fasce d'età: nella prima fascia ci sono gli scarabei con meno di un anno di vita, i piccoli; nella seconda fascia quelli che hanno più di un anno ma meno di due, gli adolescenti, e nella terza fascia quelli che anno più di due anni, i grandi. Supponiamo che i tassi dimortalità e di riproduzione siano quelli descritti dalla seguente tabella:

• la metà degli scarabei muore nel primo anno di vita
• due terzi degli scarabei che arrivano al secondo anno muoiono prima di arrivare al terzo
• nel terzo anno muoiono tutti gli scarabei ma prima di morire ne generano in medi altri 6.

Una popolazione di scarabei sarà rappresentata, in questo contesto, da un vettore numerico a tre componenti x₁, x₂, x₃ che scriviamo come vettore colonna. La prima componente rappresenta il numero di scarabei piccoli la seconda gli adolescenti e la terza il numero di scarabei maturi. L'intera popolazione sarà formata da x₁ + x₂ + x₃ individui. Supponiamo che y₁, y₂, y₃ siano gli scarabei che, sulla base delle percentuali di mortalità e riproduzione, si ritrovano dopo un anno a partire dalla popolazione iniziale x₁, x₂, x₃. Dopo un anno solo la metà dei piccoli diventa adolescente perché gli altri muoiono prima dunque y₂ = x₁/2. Anologamente solo un terzo degli adolesceti raggiungono dopo un anno la maturità e quindi y₃ = x₂/3. Quanto ai nuovi nati, solo gli scarabei maturi riescono a procrearsi e, in media, ognuno di loro ne genera 6: dunque y₁ = 6x₃. Possiamo ora rappresentare quanto descritto in modo sintetico tramite un prodotto tra una opportuna matrice A e il vettore colonna dato dalla popolazione inixiale: Precisamente abbiamo: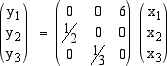

La formula precedente può essere scritta interpretando correttamente i simboli come

Se supponiamo che i tassi di crescita e mortalità della specie non cambino nel tempo, dopo due anni avremo una popolazione

In generale dopo un numero n di anni la popolazione sarà formata, nelle varie fasce d'età, da Aⁿ X individui. La popolazione è dunque destinata ad estinguersi se

In molti casi, come vedremo in seguito, è possibile calcolare il limite di matrici indicato sopra e definire la matrice esponenziale.
Si capisce facilmente come questo modello possa estendersi a popolazioni qualsiasi per le quali siano noti i tassi di mortalità e di riproduzione nelle singole fasce d'età. Se le fasce sono h e se n_i rappresenta il tasso di individui (eventualmente nullo) della fascia i che sopravive e passa alla fascia i+1 , mentre m_i è il tasso di individui (eventualmente nullo) generati dalla fascia i, allora la matrice della popolazione è:

Più in generale le matrici sono un ottimo strumento per descrivere in modo accessibile a un calcolatore una trasformazione, un processo dinamico. Generalmente un sistema, che viene "fotografato" in un dato istante, viene descritto da un stringa di numeri. Tali valori caratterizzano lo stato del sistema nell'istante preso in esame. Se pensiamo ad esempio ad una determinata regione dell'atmosfera e siamo interessati a descrivere l'evoluzione di questo sistema per fare delle previsioni metereologiche, allora potremmo descrivere la situazione che si determina in un dato istante attraverso una serie di parametri che ne caratterizzano lo stato, ad esempio la temperatura, la densità dell'aria, la pressione, l'umidità, la velocità delle molecole ecc. ecc. Una tale stringa di valori viene pensata come un vettore numerico X a n componenti, se n è il numero di parametri coi quali viene descritto il sistema. Per descrivere ora la sua dinamica basterà dire come si modifica il vettore X che lo descrive. Supponiamo di aver discretizzato il tempo, di averlo cioè diviso in intervalli discreti (di minuto in minuto, di ora in ora, di giorno in giorno ecc) e supponiamo che Y sia lo stato del sistema dopo un tale intervallo. Un modo semplice di descrivere il rapporto tra X e Y è di suppore che

dove A è una data matrice nxn. Un sistema la cui dinamica è descritta dalle equazioni precedenti si dice lineare poichè le equazioni che esprimono le y in funzione delle x sono di primo grado. Esplicitando infatti, componente per componente, la formula precedente otteniamo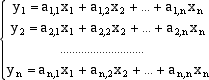

La dinamica del sistema, cioè quello che accade dopo due, tre o più istanti viene descritto, come nl caso degli scarabei, dalle potenze della matrice A. In un certo senso, in prima aprossimazione e "in piccolo", ogni sistema può pensarsi linearizzabile nello stesso modo in cui ogni funzione continua e derivabile può approssimarsi in piccolo con la sua retta tangente. Tuttavia esistono fenomeni che presentano moti turbolenti, a volte caotici il cui studio non è riconducibile a dinamiche lineari.

Le matrici di transizione
Supponiamo che il sistema che vogliamo studiare abbia un numero finito di stati: S₁, S₂, ... ,S_n che la sua evoluzione sia discreta, cioè la transizione da uno stato a quello successivo avvenga tramite passi discreti. Supponiamo che p_i,j sia la probabilità che il sistema ha di passare dallo stato S_i allo stato S_j al passo successivo. Otteniamo in questo modo una matrice quadrata P di n righe e n colonne detta matrice di transizione. Questa matrice da un modello dell'evoluzione del sistema. Anche in questa situazione il prodotto P², di P per se stessa, ha una importante interpretazione: l'elemento q_i,j della matice P² è dato da

e questo numero esprime la probabilità di passare dallo stato S_i allo stato S_j in due passi. Infatti la probabilità di passare dallo stato S_i allo stato S₁ e dallo stato S₁ allo stato S_j è il prodotto delle probabilità p_i,1p_1,j e la probabilità di passare da S_i a S_j passando da S₁, S₂, ..., S_n è la somma di tali prodotti.

Consideriamo un esempio legato alla teoria dei giochi.
Il giocatore A invita il giocatore B a giocare al seguente gioco d'azzardo. Si stabilisce una posta e si lancia a turno un dado. Le regole del gioco sono le seguneti:

• Se esece 6 si vince la posta
• Se esce 5 o 4 si ritira il dado
• Se esce 3,2,1 si passa il dado all'altro giocatore

• stato a: il giocatore A tira il dado
• stato b: il giocatore B tira il dado
• stato A: il giocatore A vince
• stato B: il giocatore B vince

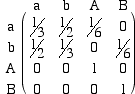Questa matrice ci serva per sapere quale è la probabilità di vincere del giocatore A rispetto al giocatore B dopo un certo numero di lanci. Calcolando, ad esempio, la matrice P⁴ otteniamo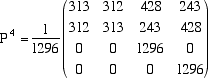

da cui risulta che la probabilità di passare dallo stato a allo stato A in 4 lanci è 428/1296 = 0.33 mentre quella di passare dallo stato a allo stato B è 243/1296 = 0.18. In altri termini il giocatore che inizia ha quasi il doppio delle probabilità del suo avversario di vincere la posta in 4 lanci. Questo esempio mostra chiaramente come il gioco che abbiamo presentato e che apparentemete sembrava equo sia invece estremamente disonesto. La conoscenza o meno di questa matematica, alla base delle moderne teorie economiche, diventa un'arma molto potente nelle mani di chi sia in grado di gestirla.

Esercizio divertente