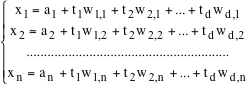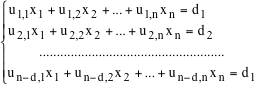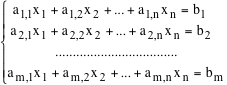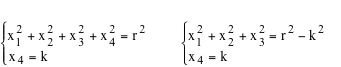|
Spazi euclidei di dimensione n
In questo capitolo generalizzeremo la geometria euclidea al caso di spazi di dimensione qualunque. Per raggiungere questo scopo, come al solito, seguiremo il metodo assiomatico deduttivo fissando dei punti di partenza e dei postulati che ci permettano di sviluppare una teoria matematica. Per fare questo dobbiamo capire quali siano state le proprietà essenziali che ci hanno permesso di introdurre i concetti base della geometria (distanza, retta, piano, parallelismo, perpemdicolarietà ecc.). E' chiaro che alla base di tutto c'è il concetto di vettore geometrico e le operazioni vettoriali tra vettori geometrici e quindi anche ora partiremo dal concetto di spazio vettoriale.
Sia dunque V uno spazio vettoriale reale di dimensione finita dotato di un prodotto scalare.
Definizione di spazio euclideo su V
Dato uno spazio vettoriale reale V dotato di un prodotto scalare, uno spazio euclideo su V, che indichiamo con E(V) o più semplicemente con E, è un insieme, i cui elementi chiamiamo punti, con una corrispondenza che associa a ogni coppia ordinata di punti A, B di E un vettore di V che denotiamo con AB in modo che siano verificati i seguenti postulati:
(1) Dati comunque tre punti A,B,C di E risulta
AB + BC = AC
(2) Dato un qualunque punto O di E e un qualunque vettore v di V esiste uno e un solo punto P di E tale che OP = v
Dalla prima assunzione risulta che AA + AA = AA e quindi, dato che in uno spazio vettoriale solo il vettore nullo è uguale al suo doppio
AA = 0 per ogni punto A di E
.
Da questo possiamo dedurre anche che AB + BA = 0 e quindi
BA = -AB per ogni coppia di punti A e B di E.
Diciamo che uno spazio euclideo E su V è di dimensione n se dim V = n.
Un esempio importante, oltre allo spazio euclideo ordinario a tre dimensioni, si ottiene quando V = Rn = E. In questo caso la corrispondenza che associa a ogni coppia ordinata di punti di Rn un vettore di Rn si ottiene per differenza:
AB = B-A dove A=(a1,a2,..., an) e B=(b1,b2,..., bn)
E' immediato verificare la validità delle condizioni (1) e (2). Lo spazio euclideo così ottenuto si chiama lo spazio euclideo numerico a n dimensioni e si indica, normalmente, con En. Occorre in questo caso non confondere la doppia natura di una n-upla ordinata di numeri che va pensata come punto, se si tratta di un elemento di En, e come vettore, se si tratta di un elemento dello spazio dei vettori di En.
Definizione di sottospazio euclideo
Sia E uno spazio euclideo su V e S un sottoinsieme di E. S è un sottospazio euclideo di E se è esso stesso uno spazio euclideo cioé se è non vuoto e il seguente insieme di vettori
WS = {AB: A, B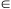 S} S}
è un sottospazio vettoriale di V e, dato un qualunque punto O di S e un vettore w di WS, esiste il punto P appartiene a S tale che OP = w.
Lo spazio WS definito sopra si chiama la giacitura di di S, e
se O 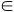 S allora OP S allora OP 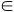 WS se e solo se P WS se e solo se P 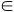 S S
Diciamo che S è di dimensione d se dim WS = d.
Sia E uno spazio euclideo di dimensione n su V. Un sottospazio euclideo di E dimensione zero è formato da un singolo punto, un sottospazio euclideo di E di dimesione uno si chiama retta, un sottospazio euclideo di E di dimensione 2 si chiama piano e un sottospazio euclideo di E di dimensione n-1 si chiama iperpiano. Per le altre dimensioni non ci sono nomi specifici.
E' facile vedere che, dato un punto A dello spazio E e un sottospazio vettoriale W di V l'insieme dei punti
S = {P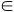 E : AP E : AP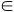 W} W}
costituisce un sottospazio euclideo di E la cui giacitura è W. Tale sottospazio si chiama il sottospazio euclideo passante per A con giacitura W. La definizione si giustifica per il fatto che il punto A appartiene a S dato che il vettore AA=0 appartiene a W essendo W un sottospazio vettoriale di V.
I sottospazi euclidei di un dato spazio euclideo possono intersecarsi tra loro e questa operazione si riflette naturalmente sulla analoga operazione sulle giaciture. Precisamente abbiamo il seguente
Teorema 1
Dati due sottospazi euclidei S e S' di uno spazio eucildeo E su V, se S e S' hanno almeno un punto in comune allora
(1) S 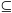 S' se e solo se WS S' se e solo se WS 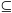 WS' WS'
(2) S  S' è un sottospazio euclideo di E e
WS S' è un sottospazio euclideo di E e
WS  S' = WS S' = WS WS' WS'
Dimostrazione
Dimostriamo (1). Se S 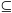 S' la cosa è ovvia. Viceversa sia O un punto comune a S e S' allora per ogni punto P in S, il vettore OP appartiene a W S e quindi anche a W S'. Ne segue che P appartiene a S'. S' la cosa è ovvia. Viceversa sia O un punto comune a S e S' allora per ogni punto P in S, il vettore OP appartiene a W S e quindi anche a W S'. Ne segue che P appartiene a S'.
Dimostriamo la (2).
Abbiamo WS  S' =
{PQ : P,Q S' =
{PQ : P,Q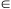 S S  S'}. Ma dato che P e Q appartengono a S il vettore PQ appartiene a WS e analogamente appartiene a WS'. Ne segue che WS S'}. Ma dato che P e Q appartengono a S il vettore PQ appartiene a WS e analogamente appartiene a WS'. Ne segue che WS  S' è contenuto in WS S' è contenuto in WS WS'. Ora se esiste un punto O comune a S e S' allora ogni vettore
w appartenente a WS WS'. Ora se esiste un punto O comune a S e S' allora ogni vettore
w appartenente a WS WS' potrà rappresentarsi con la coppia OP per qualche punto P dello spazio. Ma se w = OP appartiene a WS e O appartiene a S allora anche P deve appartenere a S. Analogamente si vede che P appartiene anche a S'. WS' potrà rappresentarsi con la coppia OP per qualche punto P dello spazio. Ma se w = OP appartiene a WS e O appartiene a S allora anche P deve appartenere a S. Analogamente si vede che P appartiene anche a S'.
Corollario
Sia S un sottospazio di dimesione d di uno spazio euclideo E di dimensione n e sia H un iperpiano che non contiene S ma che lo interseca in qualche punto. Allora S H è un sottospazio di E di dimensione d-1. H è un sottospazio di E di dimensione d-1.
Dimostrazione
Siano WS e WH le giaciture di S ed H rispettivamente. Abbiamo
dim WS = d e dim WH = n-1.
Dato che S H non è vuoto, per il teorema precedente (1), WH non contiene WS e quindi esiste un vettore di WH che non appartiene a WS ma allora, essendo V di dimensione n e WH di dimensione n-1, abbiamo H non è vuoto, per il teorema precedente (1), WH non contiene WS e quindi esiste un vettore di WH che non appartiene a WS ma allora, essendo V di dimensione n e WH di dimensione n-1, abbiamo
WS + WH = V.
Per la formula di Grassmann risulta allora
dim WS  WH = d + (n-1) -n = d-1. WH = d + (n-1) -n = d-1. e quindi, dato che S H non è vuoto, per il teorema precedente (2), S H non è vuoto, per il teorema precedente (2), S H è un sottospazio di E di dimensione d-1. H è un sottospazio di E di dimensione d-1.
Definizione di parallelismo
Due sottospazi S e S' di uno spazio euclideo E si dicono parallei se hanno la stessa giacitura.
La geometria di spazi paralleli è essenzialmente uguale a quella che vale negli spazi oridinari tridimensionali.
Osserviamo intanto che se due sottospazi paralleli hanno un punto in comune allora coincidono. Se infatti O 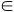 S S S' allora per ogni punto P di S,
OP S' allora per ogni punto P di S,
OP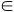 WS = WS' e dato che O appartiene anche a S' questo punto P appartiene a S'. Questo dimostra che S è contenuto in S'. L'inclusione inversa si dimostra nello stesso modo. WS = WS' e dato che O appartiene anche a S' questo punto P appartiene a S'. Questo dimostra che S è contenuto in S'. L'inclusione inversa si dimostra nello stesso modo.
Il teorema seguente da una caratterizzazione del parallelismop in termini geometrici.
Teorema 2
Siano S e S' due sottospazi paralleli di dimensione d di uno spazio euclideo E di dimensione n.
Esiste allora un sottospazio euclideo di dimensione d+1 che contiene sia S che S'.
Viceversa se i due sottoispazi di dimensione d non si intersecano e sono contenuti in uno stesso sottospazio di dimensione d+1 allora S e S' sono paralleli.
Dimostrazione
Supponiamo che S e S' siano due sottospazi paralleli. Se sono uguali sono ovviamente contenuti in un sottospazio di dimensione d+1. Supponiamo dunque che siano diversi. Sia W=WS=WS' la giacitura dei due sottospazi. Scegliamo in S d+1 punti A, A1, A2,..., Ad tali che i vettori AA1, AA2, ... , AAd siano una base di W. Sia B un punto di S' che non appartiene a S, il vettore AB non appartiene a W perchè altrimenti B sarebbe un punto di S. Lo spazio
U=Span(AA1, AA2, ... , AAd,AB) è dunque di dimensione d+1. Sia T il sottospazio euclideo di E passante per A con la giacitura U. Tale spazio contiene S dato che se P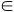 S allora AP S allora AP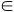 WS=W WS=W 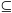 U. Ma A appartiene a T e quindi, essendo AP nella sua giacitura U, anche P deve appartenere a T. Dunque T contiene tutti i punti di S. T contiene anche S'. Infatti B U. Ma A appartiene a T e quindi, essendo AP nella sua giacitura U, anche P deve appartenere a T. Dunque T contiene tutti i punti di S. T contiene anche S'. Infatti B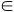 T perché A T perché A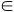 T e AB T e AB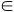 U, inoltre se Q U, inoltre se Q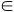 S' allora BQ S' allora BQ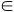 WS'=W WS'=W 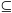 U e quindi Q appartiene a T. U e quindi Q appartiene a T.
Viceversa supponiamo che i due sottospazi non si intersechino e che siano contenuti in uno stesso sottospazio T di dimensione d+1.
S 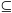 T e S' T e S' 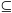 T T
Nello spazio euclideo T abbiamo due iperpiani S e S' i quali sono paralleli perché in caso contrario, come stabilisce il seguente lemma, avrebbero una intersezione non vuota.
Lemma
Sia E uno spazio euclideo su V di dimensione n e H , H' due suoi iperpiani non paralleli. In queste ipotesi i due iperpiani si intersecano lungo un sottospazio euclideo di dimensione n-2.
Dimostrazione
Siano H e H' i due iperpiani e siano WH e WH' le rispettive giaciture. Poichè dim WH = n-1 = dim WH' e i due sottospazi sono diversi essendo i due iperpiani non paralleli, abbiamo
WH + WH' = V
Sia ora A un punto di H e A' un punto di H'. Il vettore AA' essendo un vettore di V si scrive come somma di un vettore di WH e di WH'
AA' =v + v' con
v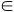 WH , v' WH , v'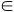 WH' WH'
Poichè A appartiene all'iperpiano H e v a WH esisteà un punto P in H tale che AP = v. Abbiamo allora AA' = AP + v' e quindi
v' = AA' - AP = AA' + PA =PA+ AA' = PA' = -A'P
Dato che A' è un punto di H' e A'P un vettore di WH',
ne segue che P è un punto di anche dell'iperpiano H'. Questo dimostra che due iperpiani non paralleli (cioè con giaciture diverse) si incontrano.
Per vedere la dimensione della loro intersezione applichiamo la formula di Grassmann
dim (WH WH') =
dim WH + dim WH' - dim(WH+WH') =
(n-1) +(n-1) - n = n-2 WH') =
dim WH + dim WH' - dim(WH+WH') =
(n-1) +(n-1) - n = n-2
La conclusione del teorema segue quindi dal teorema 1 (parte 2).
Possimo dunque concludere, come nel caso delle rette della geometria ordinaria, che due sottospazi euclidei diversi di dimensione d sono paralleli se e solo se sono contenuti in uno stesso sottospazio di dimensione d+1 e non si intersecano.
La nozione di parallelismo può essere estesa al caso di sottospazi di dimensione diversa. Sia S un sottospazio euclideo di E di dimensione d e S' un sottospazio di dimensione d' e supponiamo che d  d'. Diciamo che S è parallelo a S' se WS d'. Diciamo che S è parallelo a S' se WS 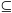 WS'. Applicando il teorema 1 possimo affermare che, se due sottospazi paralleli hanno un punto in comune, allora il più piccolo è interamente contenuto nel più grande. Inoltre, ragionando come nella dimostrazione del teorema 2, se due sottospazi paralleli di dimensioni d e d',
con d WS'. Applicando il teorema 1 possimo affermare che, se due sottospazi paralleli hanno un punto in comune, allora il più piccolo è interamente contenuto nel più grande. Inoltre, ragionando come nella dimostrazione del teorema 2, se due sottospazi paralleli di dimensioni d e d',
con d  d', non si incontrano, allora sono entrambi contenuti in uno stesso sottospazio di dimensione d'+1. Viceversa se i due sottospazi sono contenuti in uno stesso sottospazio T di dimensione d'+1 e non si incontrano allora sono paralleli infatti se WS d', non si incontrano, allora sono entrambi contenuti in uno stesso sottospazio di dimensione d'+1. Viceversa se i due sottospazi sono contenuti in uno stesso sottospazio T di dimensione d'+1 e non si incontrano allora sono paralleli infatti se WS 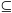 WT e WS' WT e WS' 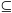 WT allora,
viste le dimensioni di questi spazi, se WS non è contenuto in WS', allora WS + WS' = WT e possiamo, ragionando come nel lemma, trovare un punto in comune a WS e WS' contraddicendo l'ipotesi. In generale dunque non è vero che se due sottospazi non si incontrano sono paralleli: per essere paralleli occorre una condizione in più, occorre che i due sottospazi siano entrambi contenuti in un sottospazio "piccolo", con una sola dimensione in più dello spazio più grande. WT allora,
viste le dimensioni di questi spazi, se WS non è contenuto in WS', allora WS + WS' = WT e possiamo, ragionando come nel lemma, trovare un punto in comune a WS e WS' contraddicendo l'ipotesi. In generale dunque non è vero che se due sottospazi non si incontrano sono paralleli: per essere paralleli occorre una condizione in più, occorre che i due sottospazi siano entrambi contenuti in un sottospazio "piccolo", con una sola dimensione in più dello spazio più grande.
Teorema 3
Sia E uno spazio euclideo di dimensione n e S e S' due sottospazi distinti tali che
dim S + dim S' = n e
dim WS  WS' = {0} WS' = {0}
allora S  S' = {P}. S' = {P}.
Dimostrazione
Dimostriamo la tesi per induzione su n. Per n = 2, siamo nella situazione del lemma.
In generale, supponiamo che sia n > 2 e
d= dim S  dim S' = d' dim S' = d'  n/2. n/2.
Prendiamo un iperpiano H che contiene S e un punto A di S'. Tale iperpiano esiste e può essere costruito nel modo seguente: scegliamo d+1 punti di S A0, A1, A2,..., Ad tali che i vettori A0A1, A0A2, ... , A0Ad siano una base di WS. Consideriamo ora i d+1 vettori
AA0, AA1, ... , AAd e sia Z un sottospazio vettoriale di V che contiene tali vettori
e che abbia dimensione n-1. Tale sottospazio esiste dato che d+1  n-1 (d n-1 (d (n/2), n>3, per n=3 d=1). Sia H l'iperpiano che passa per A e che ha come giacitura Z. Tale iperpiano contiene S ma non contiene S' dato che, in questo caso Z, conterrebbe, applicando il teorema 1 parte 1, sia WS che WS' e quindi conterrebbe la loro somma WS + WS'. Ma, per ipotesi WS (n/2), n>3, per n=3 d=1). Sia H l'iperpiano che passa per A e che ha come giacitura Z. Tale iperpiano contiene S ma non contiene S' dato che, in questo caso Z, conterrebbe, applicando il teorema 1 parte 1, sia WS che WS' e quindi conterrebbe la loro somma WS + WS'. Ma, per ipotesi WS  WS' = {0} e quindi, applicando la formula di Grasmann, la somma risulta di dimensione n mentre Z, che contiene la somma, è di dimensione n-1.
H dunque interseca S' nel punto A ma non lo contiene. Applicando il teorema 1 possiamo concludere che H interseca S' in un sttospazio euclideo S' WS' = {0} e quindi, applicando la formula di Grasmann, la somma risulta di dimensione n mentre Z, che contiene la somma, è di dimensione n-1.
H dunque interseca S' nel punto A ma non lo contiene. Applicando il teorema 1 possiamo concludere che H interseca S' in un sttospazio euclideo S'  H di dimensione d'-1.
Abbiamo in definitiva uno spazio euclideo H di dimensione n-1 che ontiene un sottospazio euclideo S di dimensione d e un sottospazio S' H di dimensione d'-1.
Abbiamo in definitiva uno spazio euclideo H di dimensione n-1 che ontiene un sottospazio euclideo S di dimensione d e un sottospazio S'  H di dimensione d'-1. Le giaciture di tali spazi non si intersecano dato che non si intersecano quello (più grandi) di S e S' H di dimensione d'-1. Le giaciture di tali spazi non si intersecano dato che non si intersecano quello (più grandi) di S e S'  H. Applicando l'ipotesi induttiva abbiamo che S e S' H. Applicando l'ipotesi induttiva abbiamo che S e S'  H si intersecano in uno e un sol punto il quale risulta quindi comune a S e S'. Infine tali sottospazi non possono avere due punti in comune P e Q perché in questo caso il vettore PQ apparterebbe, contro l'ipotesi alle due giaciture. H si intersecano in uno e un sol punto il quale risulta quindi comune a S e S'. Infine tali sottospazi non possono avere due punti in comune P e Q perché in questo caso il vettore PQ apparterebbe, contro l'ipotesi alle due giaciture.
Osserviamo, come sarà chiaro nel seguito, che questo teorema equivale, usando le coordinate, a dire che, un sistema lineare quadrato, la cui matrice dei coefficienti ha rango massimo ha sempre una e una sola soluzione.
Distanze e angoli negli iperspazi
Tutti i risultati che abbimo dimostrato fino a questo punto usano solo la struttura di spazio vettoriale di V senza usare il prodotto scalare. Essi valgono dunque in un contesto più generale di una spazio E strutturato su uno spazio vettoriale V qualunque. In questo caso la geometria che ne deriva è la geometria affine e tutti i teoremi che abbiamo dimostrato fino a questo punto sono teoremi di geometria affine. Quando invece supponiamo che su V sia definito un prodotto scalare, come abbiamo fatto in questo capitolo, abbiamo la geometria euclidea nella quale è possibile parlare di distanze e angoli che vengono definiti a partire da questa operazione.
Se A e B sono due punti la loro distanza è il numero reale positivo
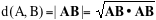
Il coseno dell'angolo tra due segmenti AB e AC sarà definito nel solito modo tramite il prodotto scalare dei vettori AB e AC.
Vediamo ora come si definisce la proiezione ortogonale di un punto P dello spazio Euclideo E su un suo sottospazio euclideo S. Sia WS = Span(f1,f2, ... , fd) la giacitura di S che abbiamo generato con una base f1,f2, ... , fd ortonormale e sia A un fissato punto di S. Consideriamo il vettore
HP = AP - [(AP.f1)f1 +(AP.f2)f2 + ... + (AP.fd)fd]
Il vettore HP è ortogonale a WS dato che
HP.fi = AP.fi - [(AP.f1)(f1.fi) + (AP.f2)(f2.fi) + ... + (AP.fd)(fd.fi) ] =
AP.fi - (AP.fi)(f1.fi)=0
per ogni i=1,2,...,d. Inoltre il punto H appartiene a S dato che
AH= AP + PH =AP - HP = (AP.f1)f1 +(AP.f2)f2 + ... + (AP.fd)fd 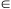 WS WS
e quindi dato che A appartiene a S anche H vi appartiene. Il punto H definito dalla relazione vettoriale precedente si chiama la proiezione ortogonale di P su S.
Questo permette anche di definire la distanza di un punto P da un sottospazio euclideo S come il modulo del vettore HP.
Definizione di ortogonalità
Dati due sottospazi euclidei S e S' di uno spazio euclideo E di dimensione n, diciamo che S è ortogonale a S' se
WS' = (WS)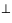 o, che è lo stesso, WS = (WS') o, che è lo stesso, WS = (WS')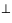
Questo significa, in particolare, che se d e d' sono le dimensioni di S e S' rispettivamente allora d'=n-d.
Dato che in uno spazio vettoriale un sottospazio interseca il suo ortogonale solo nel vettore nullo, possiamo applicare il teorema 3 e concludere che due sottospazi ortogonali tra loro, di dimensioni di e n-d, si intersecano in un punto e "invadono tutto lo spazio" non sono cioè contenuti in un sottospazio proprio di E.
Anche in questo contesto generale ritroviamo l'antico enunciato euclideo: sia T un sottospazio ortogonale a S, allora un secondo sottospazio T' è ortogonale a S se e solo se T' è parallelo a T:
(WS)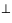 = WT, WT' = (WS) = WT, WT' = (WS)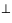 se e solo se WT'=WT se e solo se WT'=WT
La nozione di ortogonalità tra sottospazi può essere estesa anche al caso di sottospazi di dimensioni qualunque. Siano S e S' due sottospazi di dimesioni d e d' rispettivamente. Diciamo che S è ortogonale a S' se
(WS)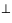 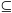 WS' (se n WS' (se n  d+d')
WS d+d')
WS 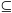 (WS')
(WS')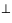 (se d+d' (se d+d'  n). n).
La definizione implica che due sottospazi ortogonali non possono mai essere paralleli dato che un vettore non può essere ortogonale a se stesso.
Nel caso, ad esmpio, di due iperpiani H e H' in uno spazio E di dimensione maggiore di 2, abbiamo che H è ortogonale a H' se e solo se
U=(WH)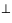 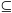 WH' WH'
Ne segue che WH' non può essere uguale a WH perché in questo caso WH conterrebbe il suo ortogonale U ed esisterebbe quindi un vettore non nullo u in U ortogonale a ogni vettore di W e in particolare ortogonale a se stesso! Due iperpiani ortogonali dunque si intersecano e la condizione di ortogonalità si riduce a dire che l'iperpiano H' contenga una retta ortogonale ad H e ritroviamo così la definizione di Euclide nel caso di due piani dello spazio ordinario tridimensionale.
Coordinate cartesiane negli spazi euclidei
Sia E uno spazio euclideo su V di dimensione n. Un sistema di coordinate cartesiane su E è una (n+1)-upla
(O,e1,e2,...,en) dove O è un punto di E, e {e1,e2,...,en} è una base ortonormale di V.
Se P è un qualunque punto di E le coordinate cartesiane di P nel dato sistema di riferimento sono le componenti del vettore OP
OP = x1e1 + x2e2 + ... +xxen e, come nel caso tridimensionale, scriviamo, con abuso di notazione, P=(x1,x2, ... , xn).
Se A =(a1,a2, ... , an) e B=(b1,b2, ... , bn) sono due qualunque punti di E, le proprietà (1) e (2) ci permettono di calcolare le componenti del vettore AB nella data base di V:
AB = AO+OB = OB - OA = (b1 - a1)e1 + (b2 - a2)e2 +... + (bn - an)en.
Sia S un sottospazio euclideo di E e sia W la sua giacitura. Fissiamo una base, non necessariamente ortonormale, {w1,w2, ... , wd} di W e un punto A=(a1,a2, ... , an) di S, allora un punto P =(x1,x2, ... , xn) dello spazio appartiene a S se e solo se
AP = t1w1 + t2w2 + ... + tdwd
Supponiamo che le componenti dei vettori w siano date da
wi = wi,1e1+wi,2e2+...+wi,nen (i=1,2,...,d)
Con questa scelta dei simboli, la condizione precedente si traduce immediatamente nelle equazioni
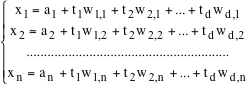
che si chiamano equazioni parametriche del sottospazio eucliedeo passante per A con giacitura W=Span(w1,w2, ... , wd).
Una descrizione alternativa passa attraverso la considerazione dello spazio ortogonale W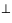 = U. Questo spazio sappiamo ha dimensione n-dim S. Sia dunque u1,u2, ... ,un-d una base (non necessariamente ortonormale) di U.
Allora un punto P dello spazio appartiene al sottospazio euclideo passante per A e con giacitura W se e solo se AP è ortogonale a ogni vettore di U= W = U. Questo spazio sappiamo ha dimensione n-dim S. Sia dunque u1,u2, ... ,un-d una base (non necessariamente ortonormale) di U.
Allora un punto P dello spazio appartiene al sottospazio euclideo passante per A e con giacitura W se e solo se AP è ortogonale a ogni vettore di U= W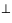 cioè se e solo se appartiene a U cioè se e solo se appartiene a U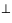 = (W = (W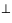 ) )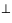 = W. Questa condizione si riduce ad annullare gli n-d prodotti scalari = W. Questa condizione si riduce ad annullare gli n-d prodotti scalari
AP .u1 = 0 , AP .u2 = 0 , ... , AP .un-d = 0
e passando alle coordinate, supponendo che
ui = ui,1e1+ui,2e2+...+ui,nen (i=1,2,...,n-d)
con lo stesso calcolo fatto nel caso tridimensionale, otteniamo
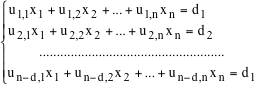
Queste equazioni si chiamo le equazioni cartesiane del sottospazio euclideo di E passante per A e ortogonale a Span(u1,u2,...,un-d). In particolare un iperpiano è definito da una equazione cartesiana
a1x1 + a2x2 +...+anxn = d
e ogni sottospazio euclideo di E di dimensione d si ottiene intersecando n-d iperpiani.
Teorema 4
Sia E uno spazio euclideo di dimensione n e sia S l'insieme dei punti P=(x1,x2,...,xn) le cui coordinate sono soluzioni di un sistema lineare.
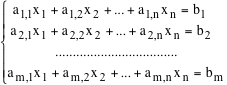
In queste ipotesi, se S è non vuoto, è un sottospazio euclideo di E e la dimensione della sua giacitura è uguale a n-r essendo r il rango della matrice dei coefficienti del sistema.
Dimostrazione
Dato che il sistema è compatibile per ipotesi, esiste almeno una soluzione A=(a1,a2,...,an). Riduciamo ora la matrice dei coefficienti del sistema con l'algoritmo di Gauss. Questa operazione non altera l'insieme delle soluzioni, ma alla fine produce un nuovo sistema ridotto formato, se d è il rango della matrice dei coefficienti, da n-d equazioni indipendenti che danno luogo a n-d vettori di V i quali generano uno spazio U di dimensione n-d. Per quanto abbiamo visto sopra, le soluzioni del sistema ridotto, danno le coordinate dei punti del sottospazio euclideo
passante per A con la giacitura W=U . .
Questo teorema permette di interpretare geometricamente le soluzioni di un qualunque sistema lineare: le soluzioni, se esistono, formano comunque un sottospazio euclideo di E ottenuto, se d è il rango della matrice dei coefficienti del sistema, intersecando n-d iperpiani.
Alcuni oggetti interessanti negli spazi euclidei di dimensione 4
Sia E uno spazio euclideo a 4 dimensioni e sia V il suo spazio di vettori. In E, abbiamo punti rette, piani e iperpiani. La geometria delle rette è uguale a quella delle rette dello spazio ordinario: due rette possono essere incidenti, parallele o, se non sono ne parallele ne incidenti, vengono dette sghembe. Nei primi due casi, e solo in quelli, le due rette appartengono a uno stesso piano mentre se sono sghembe sono contenute in un iperpiano. Questo iperpiano si costruisce scegliendo due punti A e B della prima retta e due punti A' e B' della seconda retta e prendendo lo spazio H passante per A e con la giacitura W=Span(AB,AA',AB'). H contiene le due rette perché contiene A,A',B,B', inoltre i tre vettori indicati sono linearmente indipendenti perché altrimenti H sarebbe un piano e le due rette sarebbero complanari mentre si era supposto non lo fossero.
Più interessante la situazione relativa ai piani. Siano S e S' due piani distinti e siano W e W' le due rispettive giaciture.
Si tratta di due sottospazi vettoriali di V di dimensione 2.
- Se dim(W+W')=2 (dim(W
 W')=2) allora W=W' e i due piani sono paralleli e sono quindi contenuti in uno stesso iperpiano W')=2) allora W=W' e i due piani sono paralleli e sono quindi contenuti in uno stesso iperpiano
- Se dim(W+W')=3 (dim(W
 W')=1) abbiamo due casi: W')=1) abbiamo due casi:
- i piani sono contenuti in uno stesso iperpiano e allora si incontrano in una retta
- i piani non sono contenuti in uno stesso iperpiano e allora non si intersecano e sono detti sghembi
- e dim(W+W')=4 (dim(W
 W')=0) i due piani si intersecano in un punto e non sono contenuti in uno stesso iperpiano W')=0) i due piani si intersecano in un punto e non sono contenuti in uno stesso iperpiano
Abbiamo qua un fenomeno nuovo: due piani che si intersecano solo in un punto! Ma questo può avvenire solo in uno spazio qudridimensionale
Queste cose possono essere dimostrate anche per via analitica. Fissato un sistema di coordinate cartesiane, tutti questi oggetti possono essere introdotti e studiati can equazioni e sistemi di equazioni. Una retta può essere espressa con 4 equazioni dipendenti da un parametro a partire da un suo punto A e da una base per la sua giacitura W=Span(w) oppure da 3 equazioni lineari ottenute a partire da una base per U = W = Span(u1,u2,u3). Nel primo caso scriviamo le equazioni (parametriche) della retta passante per A e parallela a W mentre nel secondo caso le equazioni (cartesiane) della retta passante per A ortogonale ad U.
Analogamente per i piani e gli iperpiani. = Span(u1,u2,u3). Nel primo caso scriviamo le equazioni (parametriche) della retta passante per A e parallela a W mentre nel secondo caso le equazioni (cartesiane) della retta passante per A ortogonale ad U.
Analogamente per i piani e gli iperpiani.
Possiamo anche introdurre e studiare oggetti curvi. Una ipersfera tridimensionale sarà definita come il luogo dei punti dello spazio a 4 dimensioni equidistanti da un punto C detto centro. Se C=(c1,c2,c3,c4) l'equazione della ipersfera è
(x1-c1)2 + (x2-c2)2 + (x3-c3)2) +(x4-c4)2 = r2
r è detto il raggio della ipersfera. Possiamo dimostrare che ogni iperpiano che ha distanza k < r dal centro della ipersfera la interseca in una sfera di raggio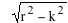 . Una ipersfera possiamo quindi immaginarla come una famiglia di sfere bidimensionali
ottenute intersecando l'ipersfera con iperpiani pralleli. Il raggio di queste sfere aumenta fino a raggiungere un massimo r per poi diminuire ulteriormente fino a zero. Infatti se scegliamo le coordinate in modo che il centro della ipersfera sia l'origine delle coordinate, la sua equazione diventa x12+ x22+ x32+ x42 = r2 e, intersecando con la famiglia di iperpiani paralleli x4=k troviamo delle sfere le cui equazioni sono . Una ipersfera possiamo quindi immaginarla come una famiglia di sfere bidimensionali
ottenute intersecando l'ipersfera con iperpiani pralleli. Il raggio di queste sfere aumenta fino a raggiungere un massimo r per poi diminuire ulteriormente fino a zero. Infatti se scegliamo le coordinate in modo che il centro della ipersfera sia l'origine delle coordinate, la sua equazione diventa x12+ x22+ x32+ x42 = r2 e, intersecando con la famiglia di iperpiani paralleli x4=k troviamo delle sfere le cui equazioni sono
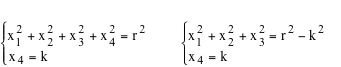
Esercizi
| |