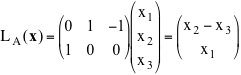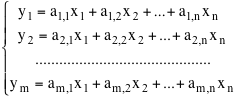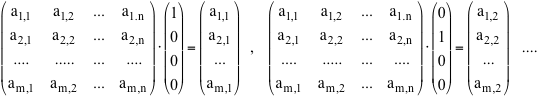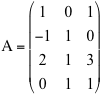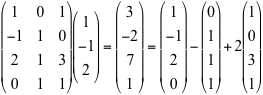|
Morfismi e matrici
In questo capitolo iniziamo lo studio di uno dei concetti portanti della matematica moderna: il concetto di morfismo. Si tratta di una idea profonda e difficile che si concretizza in moltissimi contesti e in ognuno dei quali assume un significato specifico e un nome particolare. Alla base dell'idea di morfismo (dal greco morphé: forma) c'è il concetto di applicazione (o mappa, o funzione), concetto che interviene ovunque e che in parte è già presente nella cultura matematica liceale e che ora brevemente richiamiamo. Una applicazione è definita da tre oggetti strettamente legati tra loro: un insieme X che viene detto il dominio dell'applicazione, un insieme Y che viene detto il codominio e una regola F, chiaramente definita, che permette di associare ad ogni elemento di x del dominio X un elemento y del codominio Y. Il nome che si da alla applicazione è il nome F della regola e si dice che F è una applicazione da X a Y (o anche di X in Y) e si scrive con la notazione simbolica
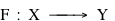 o anche o anche 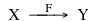
Un significato metaforico di questa scrittura è più o meno il seguente: la freccia F afferra un elemento x dall'insieme X e lo trasporta in un elemento y del codominio Y, la direzione della freccia permette di distinguere tra il dominio (da dove parte la freccia) e il codominio (dove arriva la freccia).
Un altro significato più legato al concetto di trasformazione è quello di immaginare l'applicazione come una "macchina" nella quale si inserisce un elemento x di un certo dominio X, questo oggetto entra nella macchina F, viene "frullato" e in uscita abbiamo un nuovo oggetto y di un insieme Y.
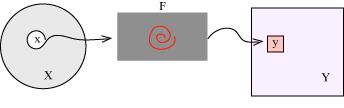
Ma la metafora forse più appropriata è quella che si lega alle proiezioni: un punto x di un insieme X si proietta in un punto y di un secondo insieme come avviene coi raggi di luce: una fonte di luce, ad esempio il sole, proietta i punti x che si trovano sul vetro della finestra in corrispondenti punti y che si trovano sul pavimento.
In generale, con riferimento a questa metafora, se F è una applicazione di X in Y e se x è un elemento del dominio il suo corrispondente y nel codominio si indica con F(x) e si chiama l'immagine di x tramite F.
Il concetto di applicazione, come ogni altro concetto matematico, non avrebbe senso se non si precisa cosa vuol dire che due applicazioni sono uguali. L'applicazione F è uguale all'applicazione G se e solo se le due applicazioni hanno lo stesso dominio, lo stesso codominio e se l'immagine di ogni punto del dominio è la stessa, cioè F(x)=G(x) per ogni x del dominio.
Le applicazioni che si considerano nei primi corsi di analisi matematica e che si incontrano già negli studi liceali sono la applicazioni di R in R e sono chiamate funzioni: x è un numero reale e la funzione è generalmente data da una espressione analitica, cioè un insieme finito di operazioni da eseguire sul numero x che, come risultato, produce in uscita un nuovo numero y. Una funzione particolarmente semplice è quella che associa a un numero x un suo multiplo ax: in questo caso l'operazione che si richiede per trovare l'immagine di un numero x è quella di moltiplicare x per una data costante a. Funzioni di questo tipo sono dette lineari perché il loro grafico, cioè i punti del piano cartesiano (x,F(x)), al variare di x nel dominio, descrivono una linea retta. In questo corso generalizziamo questo tipo di funzioni aumentando il numero di variabili e studiando a fondo la situazione che si viene a determinare quando x viene sostituito da un vettore numerico a n componenti (x1,x2,...,xn) o, più in generale, da un vettore di un generico spazio vettoriale.
A partire da una matrice A con m righe e n colonne possiamo definire una applicazione, che indichiamo col simbolo LA per evidenziare la
sua stretta dipendenza da A, di Rn in Rm nel modo seguente: trasformiamo il vettore x di Rn, che pensiamo come vettore colonna a n componenti (cioè come una matrice con n righe e 1 colonna), nel vettore y di Rm, che pensiamo pure come vettore colonna a m componenti (cioè come una matrice con m righe e 1 colonna), ottenuto moltiplicando (righe per colonne) la matrice A per la matrice x:
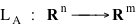
y = LA(x) = A.x
Se, ad esempio, la matrice A data da
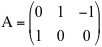
l'applicazione che essa definisce è una applicazione da R3 a R2 che trasforma il generico vettore (colonna) x di R3 nel vettore (colonna) y di R2 ottenuto moltiplicando A per x:
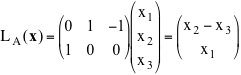
E' spesso comodo scrivere la trasformazione nel modo seguente
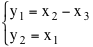
nella quale risulta chiaramente quali operazioni si devono fare sulla terna (x1,x2,x3) per ottenere la coppia (y1,y2).
In generale l'applicazione LA definita da una matrice A di m righe e n colonne da Rn a Rm può scriversi nel modo seguente:
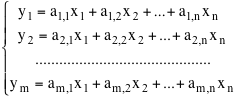
Le equazioni precedenti si chiamano anche le equazioni dell'applicazione LA
e permettono, essendo A nota, di scrivere facilmente l'immagine di un determinato vettore x di Rn.
Una proprietà di base delle applicazioni è il fatto che esse possono, in un certo senso, applicarsi più volte. Se F è una applicazione di X in Y e G una applicazione di Y in Z possiamo comporre la due applicazioni ottenendo una nuova applicazione da X a Z: un elemento x di X viene trasformato con F trovando così un elemento F(x) di Y il quale viene a sua volta trasformato con G ottenendo, in definitiva, a partire da x, l'elemento G(F(x)) che è un elemento di Z. La notazione con le frecce rappresenta bene questa situazione: dato che il codominio Y di F è uguale al dominio di G viene scritto una volta sola
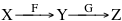
Il diagramma indica che l'applicazione F è capace di trasformare ogni elemento di X in un elemento di Y e l'applicazione G ogni elemento di Y in un elemento di Z. Questo ci permette di passare da X a Z attraverso Y applicando prima F e poi G. Il digramma con le frecce rende visibile questa situazione. L'applicazione risultante da X a Z si indica con GoF (attenzione all'ordine dei fattori) e la sua definizione è
GoF(x)=G(F(x))
Dato che questa operazione consiste nell'eseguire determinate operazioni una dopo l'altra ci aspettiamo che, avendo tre o più applicazioni, il risultato che si ottiene in ultimo sia indipendente dal modo col quale arriviamo alla fine
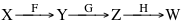
Il effetti la composizione di applicazioni è associativa, cioè
Ho(GoF) = (HoG)oF
dato che, qualunque sia il modo col quale associamo le tre applicazioni, il risultato finale è sempre H(G(F(x)).
La composizione di applicazioni riprende, generalizza e chiarisce, in un contesto più astratto, il concetto di funzione composta già incontrato nei corsi liceali: in quel caso, quando il dominio e il codominio delle funzioni è il medesimo insieme R, si possono sempre comporre due funzioni. In generale se consideriamo applicazioni di X in X (applicazioni per i quali il dominio è uguale al codominio) possiamo comporre due applicazioni F e G e il risultato è ancora una applicazione di X in X. Questa composizione di applicazioni diventa interessante anche perché è, in un certo senso, analoga al prodotto tra numeri. Oltre a essere associativa , anche in questo caso esiste una applicazione "neutra", una trasformazione che non trasforma nulla, del tutto analogo al numero 1,l'applicazione identica di X in X. Tale applicazione è generalmente indicata col simbolo Id (applicazione identica) e traforma x in x.
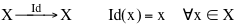
essa, comunque si scelga l'applicazione F, verifica le relazioni
FoId = IdoF= F
dato che (FoId)(x) = F(Id(x))=F(x)=Id(F(x)=(IdoF)(x) per ogni x del dominio.
Osserviamo che l'operazione di composizione tra applicazioni ci appare oltre che analoga al prodotto tra numeri, ancor più analoga al prodotto tra matrici. Anche in quel caso il prodotto non è sempre definito e anche per le matrici è importante l'ordine dei fattori che vengono moltiplicati tra l'oro ed esiste una matrice identica che interpreta il ruolo del numero 1. In realtà l'analogia non è casuale ma si precisa puntualmente se pensiamo la matrice A come una applicazione. In effetti se LA e LB sono le due applicazioni associate alle due matrici A e B , allora il codominio di LA è uguale al dominio di LB se e solo se il numero delle righe di A è uguale al numero delle colonne di B ed è precisamente questo il caso in cui il prodotto BA delle due matrici è definito.
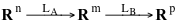
Non solo ma abbiamo l'importante relazione
LB.A = LB o LA
Per verificare che le due applicazioni sono identiche dobbiamo verificare che agiscono nello stesso modo su tutti i vettori x del dominio Rn. Usando la proprietà associativa del prodotto tra matrici abbiamo infatti:
LB.A(x) = (B.A).x = B.(A.x) = B.LA(x) = LB(LA(x))
Altre proprietà dell'algebra delle matrici si traducono, in questo contesto, in significative proprietà dell'algebra delle applicazioni. Se I è la matrice identità nxn abbiamo che
LI = Id
infatti se x è un qualunque vettore (colonna) di Rn, allora LI(x) = I.x = x = Id(x) e dunque l'applicazione LI è identica alla applicazione Id.
In più, sapendo che A.(x+x') = A.x + A.x' e che A.(ax) =a(A.x) per ogni scelta dello scalare a, ricaviamo nel contesto delle applicazioni, le due seguenti fondamentali proprietà dell'applicazione LA:
(1) LA(x + x') = LA(x) + LA(x')
(2) LA(ax) = a LA(x)
proprietà valide per ogni scelta dei vettori x e x' in Rn e per ogni scalare a in R
Queste proprietà hanno un significato particolare e sono a fondamento del concetto di morfismo lineare. Nel caso che stiamo trattando, il dominio Rn e il codominio Rm non sono semplici insiemi ma hanno una struttura più ricca che permette di fare delle operazioni vettoriali con gli elementi di questi insiemi. Come vedremo dettagliatamente più avanti, le proprietà (1) e (2) esprimono proprio il fatto che l'applicazione LA conserva la struttura, mantiene la forma. In questo senso LA non è solo una applicazione è una applicazione che conserva la struttura di spazio vettoriale, è un morfismo tra spazi vettoriali. In questo corso chiameremo i morfismi tra spazi vettoriali applicazioni lineari.
Il concetto di morfismo, come abbiamo detto, è un concetto fondamentale nella matematica moderna a un livello di astrazione maggiore di ogni altro concetto introdotto fino a questo punto. La sua comprensione non può considerarsi soddisfacente se non se ne vedono con chiarezza alcune applicazioni più concrete, se non si riesce, almeno nei casi più semplici, a formare delle immagini mentali capaci di rappresentare intuitivamente le diverse situazioni e guidare il pensiero. Questo capitolo e i successivi sono dedicati ad illustrare e discutere un primo e più semplice tipo di morfismo nel contesto specifico degli spazi vettoriali.
Tornando a considerare il morfismo LA(x), è interessante notare come esso agisce sui vettori della base canonica di Rn perché
questo mette in relazione la trasformazione con gli elementi costitutivi della matrice. Indichiamo con e1, e2, ... ,en i vettori della base canonica di Rn : eseguendo il prodotto A.e1 , A.e2 , ... ,A.enotteniamo
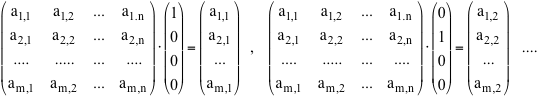
cioè, in generale, l'immagine dell'i-esimo vettore ei della base canonica di Rn è la i-esima
colonna ci della matrice A
LA(ei) = ci
Questa osservazione proprio perché LA non è una semplice applicazione ma è un morfismo, ci permette di calcolare facilmente l'immagine di un qualunque vettore x di Rn sfruttando il fatto che x è combinazione lineare dei vettori della base canonica. Abbiamo infatti x = x1e1 +
x2e2 + ... + xnen, e, usando le proprietà (1) e (2), abbiamo
LA(x) = LA(x1e1 +
x2e2 + ... + xnen) =
x1 LA(e1) +
x2 LA(e2) + ... + xn LA(en) =
= x1c1 +
x2c2 + ... + xncn
Questo calcolo mostra che l'immagine LA(x) di ogni vettore di Rn è una combinazione lineare delle colonne
della matrice A. Se denotiamo con Im LA in sottospazio di Rm costituito da tutte le immagini, tramite LA, dei vettori
x di Rn abbiamo la seguente importante descrizione:
Im LA = Span(c1, c2 , ... , cn)
Esempio
Consideriamo la seguente matrice con 4 righe e 3 colonne
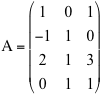
A definisce una trasformazione LA di R3 in R4 che trasforma il vettore colonna
x di R3 nel vettore colonna y = A.x di R4;
l'immagine, ad esempio, del vettore x = e1 - e2 + 2e3 che si calcola facendo il prodotto A.x è uguale a c1 - c2 + 2c3
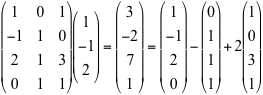
L'immagine del morfismo LA è il sottospazio di R4 generato dalle tre colonne di A. Poichè, come si vede subito, la terza
colonna è la somma delle prime due, possiamo anche osservare che
Im LA = Span(c1,c2,c3)=Span(c1,c2)
e quindi dim (Im LA) = 2. In particolare LA(e1 - e2 + 2e3) =
c1 - c2 + 2c3 =
3c1 + c2 è combinazione lineare delle prime due colonne di A.
Esercizi
| |