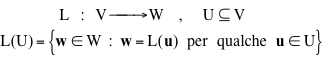|
Applicazioni lineari
Le applicazioni lineari sono i particolari tipi di morfismi che intervengono nel contesto degli spazi vettoriali. Esse vengono chiamate anche trasformazioni lineari o operatori lineari o morfismi tra spazi vettoriali. La cosa essenziale è la proprietà di linearità che è espressa da due condizioni di tipo qualitativo.
Definizione di applicazione lineare tra due spazi vettoriali
Dati due spazi vettoriali V e W su un campo di scalari K (anche finito), una applicazione lineare L di V in W
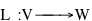
è una applicazione di V in W
tale che
(1) L(u + v) = L(u) + L(v)
(2) L(au) = a L(x)
per ogni scelta dei vettori u e v in V e per ogni scalare a in K.
Le due condizioni che abbiamo messo a fondamento del concetto di applicazione lineare chiariscono il significato del termine morfismo. Tra tutte le applicazioni tra due spazi vettoriali i morfismi sono quelle applicazioni che conservano la struttura. Dato che la struttura di spazio vettoriale è data dalla presenza di due operazioni, la somma e il prodotto per uno scalare, un morfismo di spazi vettoriali è una applicazione che conserva queste due operazioni, una applicazione cioè che conserva la somma (l'immagine di una somma è la somma delle immagini) e che conserva il prodotto per uno scalare (l'immagine del prodotto di un vettore per uno scalare è il prodotto di quello scalare per l'immagine del vettore).
Queste due proprietà di conservazione implicano altre tre importanti proprietà di conservazione.
- Una applicazione lineare L conserva il vettore nullo
(dimostrazione)
L(0) = 0
- Una applicazione lineare L conserva le combinazioni lineari
(dimostrazione)
L(a1v1 + a2v2 + ... + anvn) =
a1L(v1) + a2L(v2) + ,..., + anL(vn)
In particolare se v1, v2,... , vn sono linearmente dipendenti anche L(v1), L(v2), ... , L(vn) sono linearmente dipendenti. La stessa cosa non vale per vettori linearmente indipendenti: può cioè capitare, come vedremo meglio, che vettori linearmente indipendenti si trasformino in vettori linearmente dipendenti.
- Una applicazione lineare L conserva i sottospazi
(dimostrazione).
Ciò significa che se U è un sottospazio vettoriale di V e se L(U) è l'insieme delle immagini dei vettori di U, allora L(U) è un sottospazio vettorile di W. In formule
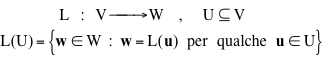
In particolare L(V) è un importante sottospazio di W che si chiama l'immagine di L e si denota con Im L.
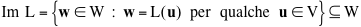
Le proprietà che abbiamo visto ci permettono di calcolare l'immagine di ogni vettore di V tramite una applicazione L sapendo che l'applicazione è lineare e sapendo come questa agisce sui vettori di una base. Siano e1, e2, ... , en i vettori di una base di V,
un generico vettore v di V si scrive come combinazione lineare dei vettori della base e dunque, se L è lineare,
deve essere
L(v) = L(x1e1 + x2e2 + ... + xnen) =
x1L(e1) + x2L(e2) + ,..., + xnL(en)
questo ci dice che possiamo calcolare L(v) conoscendo le componenti x1, x2, ... , xn di v e le immagini
in W L(e1), L(e2), ... , L(en) dei vettori della base.
Esempio
Supponiamo che V sia lo spazio dei vettori geometrici di un piano, una applicazione lineare L di V in V è determinata sapendo come L agisce sui vettori i e
j di una data base di V. Nella figura animata seguente
possiamo modificare col mouse i vettori L(i) = e , L(j) = f. Fissati questi due vettori
possiamo calcolare L(OP) per un generico vettore OP (che possiamo modificare agendo su P), calcolando le componenti lungo i e j di OP e riportando tali componenti lungo e ed f. Precisamente, se OP = xi + yj, L(OP) = xL(i) + yL(j) = xe + yf e dunque basterà calcolare i vettori xe e yf e sommarli, cosa possibile conoscendo x,y e, f.
Il programma che anima la figura fa esattamente questo calcolo: fissati e e f, dato P, calcola L(OP). Possiamo anche
vedere l'immagine una generica circonferenza (rossa) descritta dal punto P a seconda della scelta dei vettori e ed f.
Applicazioni lineari di Rn in Rm
Siamo ora in grado di descrivere tutte le applicazioni lineari di Rn in Rm . Come abbiamo visto una matrice A di m righe e n colonne individua l'applicazione LA di Rn in Rm che trasforma il generico vettore x (pensato come una matrice di n righe e 1 colonna) nel vettore A.x ottenuto moltiplicando la matrice A con la matrice x. Questa applicazione risulta lineare e fornisce quindi un importante e concreto esempio di applicazione lineare tra spazi vettoriali. La cosa ora molto importante è che non esistono altre applicazioni lineari di Rn in Rm . In altri termini, se supponiamo che una applicazione
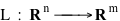
sia lineare, cioè verifichi le proprietà (1) e (2), allora, di questa trasformazione, siamo in grado di scriverne le equazioni. Precisamente sussiste il seguente
teorema che caratterizza tutte le trasformazioni linari di Rn in Rm
Teorema
Se L è una applicazione lineare di Rn in Rm allora esiste ed è unica una matrice A tale che L = LA.
Inoltre la matrice A è la matrice che ha per
colonne le immagini dei vettori della base canonica di Rn.
Dimostrazione
Sia e1, e2, ... , en la base canonica di Rn. Trasformiamo tali vettori
con la applicazione lineare L : otteniamo n vettori di Rm : c1 = L(e1) ,
c2 = L(e2) , ... , cn = L(en). Sia ora x = x1e1 +
x2e2 + ... + xnen un generico vettore di Rn , possiamo calcolare, usando le proprietà
(1) e (2) l'immagine L(x):
L(x) = L(x1e1 + x2e2 + ...
+ xnen)
= L(x1e1) + L(x2e2) + ... + L(xnen)
=
= x1L(e1) + x2L(e2) + .. +xnL(en) =
x1c1 + x2c2 + ... + xncn
Formiamo ora la matrice A che ha come colonne i vettori c1, c2, ... , cn
di Rm. Otteniamo una matrice di m righe e n colonne che definisce quindi una applicazione lineare LA di Rn in
Rm. Poichè, come abbiamo visto sopra, LA(x) =
x1c1 + x2c2 + ... + xncn = L(x) per ogni x di
Rn abbiamo che le due trasformazioni coincidono, cioè L = LA.
Esempio
Supponiamo di fare dei frullati usando solo tre tipi di frutta: banane, mele e pere e supponiamo che un frullatore riesca a sbucciare la frutta e a frullarla producendo in uscitala buccia da una parte e il succo dall'altra. Possiamo modellare questa situazione in termini di applicazioni lineari. Rappresentiamo la frutta che si vuole frullare con un vettore a tre componenti: x1 è la quantità di banane, x2 la quantità di mele e x3 quella di pere. Misuriamo la frutta in chilogrammi. Un vettore a due componenti misura la buccia e il succo:
y1 è la quantità complessiva di bucce (misurata in chilogrammi) e y2
la quantità di succo misurato in litri. La trasformazione della frutta in bucce e succo possiamo rappresentarla con una applicazione L di R3 in R2. È ragionevole pensare che L sia lineare cioè che le bucce e il succo che si ottiene
sommando due terne u e v di frutta sia la somma delle bucce e del frullato che si ottiene con la terna u e con la terna v. Ugualmente se raddoppiamo o triplichiamo o moltiplichiamo per uno scalare a i tre tipi di frutta di una terna u le bucce e il succo ottenuto sarà raddoppiato, triplicato, moltiplicato per a. Il teorema precedente ci dice che possiamo in queste ipotesi, prevedere il risultato di un qualunque frullato (quanto succo e quante bucce) eseguendo 3 soli frullati. Per fare questo basta trovare la matrice A che rappresenta l'applicazione lineare L e scrivere le equazioni della trasformazione. Seguendo la dimostrazione del teorema basta calcolare
L(e1), L(e2), L(e3). Per calcolare L(e1) dobbiamo frullare 1 chilo di banane 0 chili di mele e 0 chili di pere e vedere cosa risulta. Supponiamo che risulti 0,4 di bucce e 0,6 di succo. Questi due numeri sono la prima colonna della matrice che cerchiamo. Supponiamo che per un chilo di mele risulti 0,2 di bucce e 0,8 di succo e per le pere 0,3 di bucce e 0,7 di succo. La matrice A dell'applicazione L è la matrice
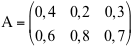
Usando questa matrice possiamo dire quanto succo e quante bucce si produrranno per una qualunque quantità frutta. Infatti per una quantità x1 di banane, x2 de mele e x3 di pere, si produrrà la quantità di bucce y1 e la quantità di succo y2 risultante dalle equazioni
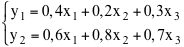
| |