Lezioni di Geometria

Franco Ghione



Rango per righe e rango per colonne di una matrice.


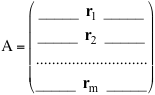Data una matrice A di m righe e n colonne abbiamo definito il rango per righe di A il massimo numero di righe della matrice linearmente indipendenti. Le righe r1, r2, ... ,rm della matrice sono vettori numerici a n componenti e sono quindi elementi dello spazio vettoriale Rn.

Esse generano il sottospazio V=Span(r1,r2, ... ,rm) la cui dimensione è appunto il rango per righe della matrice A. L'algoritmo di Gauss ci permette di calcolare questa dimensione modificando la matrice con operazioni sulle righe che non alterano lo spazio V fino ad arrivare a una matrice ridotta le cui righe non nulle sono banalmente linearmente indipendenti. A un livello più profondo possiamo ora pensare alla matrice A come a una trasformazione lineare

che trasforma il vettore (colonna) x di Rn nel vettore (colonna) y di Rm ottenuto moltiplicando A per x:

LA(x) =y= A.x

Applicchiamo il teorema di struttura a questa applicazione lineare. Cominciamo a calcolare il nucleo: Ker LA = {x Rn : Ax = 0}. Il nucleo è dunque lo spazio vettoriale costituito dalle soluzioni del sistema lineare omogeneo Ax = 0. Se r è il rango per righe della matrice A abbiamo che

dim Ker LA = n-r

Applicando il teorema di struttura otteniamo che

dim Im LA + dim Ker LA = dim Rn

e quindi

dim Im LA = r

D'altra parte l'immagine dell'applicazione lineare LA è uguale al sottospazio di Rm generato dalle colonne di A e quindi, indicando con c1, c2, ... , cn le n colonne della matrice A abbiamo

dim Im LA = r = dim Span(c1,c2, ... ,cn)

Ma la dimensione di questo ultimo spazio è dato dal massimo numero di colonne linearmente indipendenti. Possiamo concludere con questo importante risultato.

Teorema
In una qualunque matrice A il massimo numero di righe linearmente indipendente è uguale al massimo numero di colonne linearmente indipendenti.

Questo massimo numero di righe (o di colonne) linearmente indipendenti di una matrice A si chiama rango della matrice.


Il teorema di Rouché-Capelli.

Questo teorema è il teorema conclusivo e più generale sui sistemi di equazioni lineari. Un sistema lineare di m equazioni in n incognite ha la forma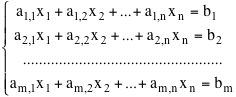


La matrice A =((ai,j)) i=1,2,...,m e j=1,2,...,n di m righe e n colonne si chiama la matrice dei coefficienti, la colonna b=((bi)) si chiama la colonna dei termini noti. Se b=0 il sistema si dice omogeneo. La matrice ((A|b)) ottenuta aggiungendo ad A la colonna dei termini notoa sichiama matrice completa del sistema. Il problema consiste nel dire in quali casi, dati A e B il sistema è compatibile, cioè ammette soluzioni, e, in questo caso dire quante sono le soluzioni e dare un algoritmo per trovarle e descriverle tutte. Il teorema di Rouché- Capelli risolve questi problemi.

Teorema (Rouché-Capelli)
Un sistema di equazioni lineari in m equazioni e n incognite è compatibile se e solo se il rango r della matrice A è uguale al rango della matrice completa ((A|b)). Nel caso in cui il sistema sia compatibile le soluzioni sono n-r e si ottengono sommando una soluzione particolare del sistema non omogeneo con un qualunque soluzione del sistema omogeneo che ha la stessa matrice A dei coefficienti.

Dimostrazione
La dimostrazione è una conseguenza della teoria generale sulle fibre di una applicazione lineare. Pensiamo le incognite come un vettore colonna x a n componenti e consideriamo l'applicazione lineare LA associata alla matrice A che trasforma x in Ax. Le soluzione del sistema sono i vettori della fibra di LA relativa vettore b pensato come vettore colonna a m componenti. Il sistema è compatibile se e solo se questa fibra è non vuota e questo accade se e solo se il vettore b appartiene all'immagine di LA. Ma sappiamo che l'immagine di LA è lo spazio generato dalle colonne della matrice A. Dunque il sistema è compatibile se e solo se la colonna b è combinazione lineare delle colonne c1,c2, ... ,cn della matrice A. Questo significa che

Span(c1,c2, ... ,cn)= Span(c1,c2, ... ,cn,b)

e quindi questi due spazi hanno la stessa dimensione. In questo caso il rango per colonne della matrice A è uguale al rango per colonne della matrice ((A|b)) e, dato che il rango per colonne di una matrice è uguale al rango della matrice, questo conclude la prima parte della dimostrazione. Supponiamo ora che il sistema sia compatibile. In questo caso le soluzioni sono i vettori della fibra su b di LA. Il teorema sulle fibre ci dice quanti sono questi vettori: essi sono 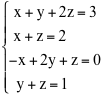k dove k=dim Ker LA = dim V - dim Im LA = n-r. La descrizione delle soluzioni come somma di una soluzione particolare con un soluzione del sistema omogeneo è una diretta rilettura del teorema sulle fibre.

Un modo rapido per risolvere il sistema consiste nel fare operazioni elementari sulle righe della matrice completa ((A|b)) fino a trovare una matrice ridotta. Le operazioni elementari non cambiano le soluzioni nel senso che se x è una soluzione del sistema Ax=b e se ((A'|b')) è una matrice ridotta di ((A|b)) allora x è anche soluzione del sistema ridotto A'x=b'.

Esempio
Consideriamo il seguente sistema in 4 equazioni e tre incognite.

riduciamo la matrice completa del sistema tenendo nota della colonna dei termini noti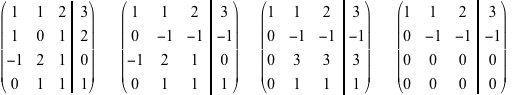

La matrice ridotta che abbiamo ottenuto da luogo al nuovo sistema molto più semplice del precedente, che ha le stesse soluzioni del sistema di partenza.

Possiamo risolvere facilmente questo sistema ridotto: la variabile libera è la z e, partendo dal basso, troviamo z=t, y=1-t, x=3-y-2z = 3-(1-t)-2t=2-t. La soluzione particolare del sistema non omogeneo è (2,1,0) e la soluzione generica sistema omogeneo è t(-1,-1,1). Il sistema ha dunque ha dunque 1 soluzioni e la soluzione generale ha la forma (x,y,z)=(2,1,0)+t(-1,-1,1).
Interpretando geometricamente questo calcolo abbiamo un esempio di 4 piani che si intersecano in una retta.

Esercizi