|
Lezioni di Geometria Franco Ghione |
 |
Automorfismi e matrici inverse
Una tipologia di morfismi particolarmente interessante si ha quando il dominio e il codominio sono lo stesso spazio vettoriale: in questo caso il morfismo si chiama endomorfismo. Uno dei motivi di interesse è che la composizione di due endomorfismi è sempre definita ed è possibile iterare più volte una applicazione lineare di questo tipo. Il teorema di struttura nel caso degli endomorfismi ha interessanti conseguenze.
 una applicazione lineare di V in V . Le condizioni seguenti sono equivalenti
La dimostrazione consiste nel dimostrare che una qualunque di queste condizioni si verifica se e solo se se ne verifica un'altra. Questo è una semplice applicazione del teorema di struttura. Abbiamo intanto già visto che Ker L = {0} se e solo se L è iniettiva. Ker L = {0} se e solo se dim Ker L = 0 se e solo se dim V = dim Im L + dim Ker L = dim Im L e questo accade se e solo se V = Im L, cioè L è suriettiva. Dunque se L è suriettiva è anche iniettiva ed è quindi biunivoca e viceversa. Infine la biunivocità è in generale equivalente al fatto che L sia invertibile. Endomorfismi che verificano queste condizioni sono detti automorfismi Questo teorema ha una interessante interpretazione nel caso in cui V=Rn. Un endomorfismo LA di Rn è definito da una matrice con lo stesso numero di righe e colonne (matrici di questo tipo sono dette quadrate) e per queste matrici sussiste il notevole risultato Corollario Una matrice di n righe e n colonne è invertibile se e solo se il suo rango è n. La matrice A è invertibile se e solo se il morfismo LA è invertibile e questo avviene se e solo se dim Ker LA=0. D'altra parte, se r è il rango della matrice A, abbiamo visto che dim Ker LA = n-r. La condizione precedente può essere verificata riducendo la matrice con l'algoritmo di Gauss per calcolare il suo rango o anche, come vedremo, calcolando il suo determinante. Il determinante di A misura se la matrice è o no invertibile: det A = 0 se e solo se A non è invertibile. Le matrici quadrate non invertibili sono anche dette matrici singolari, non singolari le altre. Ricordiamo che, dire che la matrice A è invertibile significa dire che esiste una matrice n x n, che si indica con A-1, tale che dove I è la matrice identica n x n: quella che ha 1 sulla diagonale principale e zero altrove e che, rispetto al prodotto, nell'algebra delle matrici quadrate, si comporta come il numero 1.
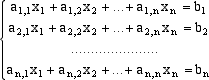 Il problema consiste, dati i coefficienti e i termini noti, nel trovare, se esistono, dei numeri x1, x2, ... ,xn che verifichino contemporaneamente le n equazioni date. Utilizzando il linguaggio e l'algebra delle matrici la scrittura precedente può essere compattata nella semplicissima forma dove il simbolo A rappresenta la matrice nxn i cui elementi sono i coefficienti del sistema, b la matrice (o vettore colonna) di n righe e 1 colonna formata dai termini noti e x l'analogo vettore colonna formato dalle n incognite. 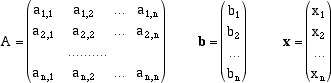 La scrittura matriciale non solo permette di compattare l'informazione, essa permette anche, per via analogica, di intuire il metodo risolutivo. Se infatti n=1 l'equazione ax = b si risolve (se a è invertibile, cioè se a è non nullo) moltiplicando ambo i membri per a-1 isolando così la x = a-1b . La stessa situazione si ripresenta nel caso generale. Se infatti la matrice A è invertibile, allora esiste una matrice A-1 e possiamo, anche in questo caso, moltiplicare a sinistra per A-1 ed, essendo anche il prodotto tra matrici associativo, come l'ordinaria moltiplicazione e quindi, dato che I si comporta come il numero 1 E abbiamo trovato l'incognita! Algoritmo di Gauss per invertire una matrice invertibile
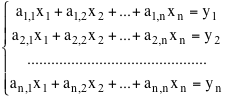 e il problema consiste, viceversa, dato il vettore y di calcolare il corrispondente vettore x, cioè dei numeri x1, x2, ... ,xn funzioni delle y, che verifichino le equazioni precedenti. L'idea dell'algoritmo consiste nel pensare il sistema precedente come un sistema omogeneo di n equazioni nelle 2n incognite x1, x2, ... ,xn e y1, y2, ... ,yn.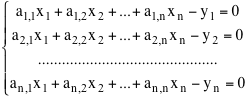 
La matrice di questo sistema è la matrice
nx2n formata dalla matrice A e dalla matrice identità cambiata di segno. Questa matrice ha rango n e il sistema ammette 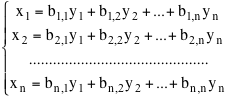 Ma, se per ogni x risulta y = A.x e x = B.y allora I.x=x = B.y =B.(A.x)=(B.A).x e quindi, dato che le due matrici I e BA moltiplicate per qualunque vettore x producono lo stesso risultato, abbiamo B.A=I e dunque, moltiplicando a sinistra per A-1, B(AA-1)= A-1 cioè B= A-1. La matrice B così ottenuta è la matrice inversa di A Per passare da A a B basterà quindi ridurre la matrice di n righe e 2n colonne  arrivando alla matrice 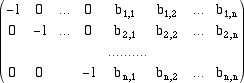 che permette di esprimere le soluzioni x in funzione delle variabili y che ora prendiamo come variabili libere.
Questa riduzione è possibile proprio perché A è di rango massimo e quindi la riduzione porta a n pivot non nulli. Le operazioni elementari consentite sono: sostituire una riga con un suo multiplo non nullo, sostituire una riga con quella riga più un multiplo di un'altra riga,permutare due righe. 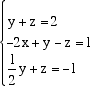 La matrice da ridurre è la matrice 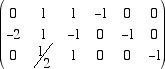 Permutando le prime due righe abbiamo 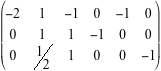 Cominciamo ora a fare operazioni elementari per produrre zeri sotto i pivot delle prime tre colonne 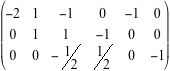 Osserviamo che, essendo la matrice dei coefficienti di rango tre, le tre colonne sono indipendenti e quindi otteniamo sempre, a questo punto della riduzione, una matrice con tutti zeri sotto la diagonale principale. Moltiplicando la prima riga per 1/2, la seconda per -1 e la terza per-2, otteniamo una matrice che tutti i pivot uguali a -1. 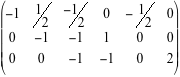 Ora, a partire dall'ultima riga, facciamo altre operazioni elementari per ottenere degli zeri sopra i pivot e arrivare alla fine, a sinistra, alla matrice -I. Moltiplichiamo quindi l'ultima riga per -1 e sommiamola alla seconda, e poi moltiplichiamo l'ultima riga per -1/2 e sommiamola alla prima, per avere gli zeri sopra il pivot della terza colonna: 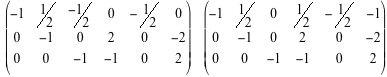 Non ci resta che sistemare la seconda colonna. Moltiplichiamo la seconda riga per 1/2 e sommiamola alla prima 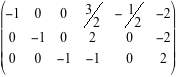 In definitiva 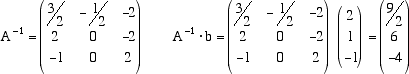 e la soluzione del sistema proposto è x=9/2, y=6, z=-4.
|
n soluzioni. Se ordiniamo le incognite scrivendo prima le y e poi le x la matrice del sistema è già ridotta e possiamo risolverlo prendendo le x come variabili libere. Le soluzioni si presentano nella forma y = A.x. Possiamo però cercare di esprimere le soluzione dello stesso sistema prendendo le y come variabili libere. In questo caso le x saranno in funzione delle y e le soluzioni si presenteranno nella forma x = B.y.