Le operazioni tra questi due elementi si eseguono seguendo le seguenti regole:

Dato che abbiamo solo due elementi si vede subito che valgono le proprietà associative commutative e distributive. Inoltre esiste sempre l'opposto dato che l'opposto di 0 è 0 (la relazione x+0=0 è soddisfatta per x=0) e l'opposto di 1 è 1 (la relazione x+1=0 è soddisfatta da x=1). Analogamente l'unico elemento non nullo del campo è 1 che ha come inverso 1 stesso dato che 1.1=1. Il nostro insieme F si comporta formalmente come gli ordinari numeri dell'aritmetica elementare. Le operazioni diventano, avendo solo due "numeri" coi quali operare, molto più semplici: ad esempio esiste un solo "numero" diverso da x: questo è il "numero" x+1!

la teoria degli spazi vettoriali sul campo F può essere sviluppatata senza problemi. Lo spazio Fⁿ dei vettori numerici a n componenti sarà definito nel solito modo

Fⁿ = {(x₁,x₂,...,x_n) : x_i F}

I vettori di questo spazio sono dunque le stringhe di zeri ed uno di lunghezza n. Poiché posso scegliere x₁ in due modi possibili, x₂ in due modi possibili indipendenti da quelli, le stringhe di lunghezza due sono 2.2=4. In generale le stringhe di lunghezza n sono 2ⁿ e dunque Fⁿ è uno spazio vettoriale con un numero finito di vettori. In generale se V è uno spazio vettoriale sul campo F di dimensione n allora ogni vettore di V si scrive in modo unico come combinazione lineare di n vettori della base, ed essendo i coefficienti della combnazione lineare 0 o 1, vi sono 2ⁿ possibili combinazioni lineari e dunque V ha 2ⁿ vettori.

Osserviamo che, in questo caso, due vettori sono linearmente dipendenti se e solo se sono uguali, e tre vettori a due a due diversi, sono linearmente dipendenti se e solo se la loro somma è zero. In generale un sistema di k vettori è un insieme di vettori linearmente dipendenti se e solo se esiste un sottosistema di vettori la cui somma è 0.


Il riconoscimento di un segnale

In questo paragrafo presentiamo un metodo, dovuto a Hamming, per individuare la presenza di un rumore che si produca durante la trasmissione di un segnale e, se il rumore è abbastanza piccolo, eliminarlo e, di conseguenza, ricostruire esattamente il segnale trasmesso. Questo metodo si serve di spazi vettoriali sul campo F con due elementi ed è di estrema importanza in molte applicazioni della matematica all'informatica. Lo portiamo ad esempio per fornire allo studente una prima semplice applicazione di questi concetti.

Supponiamo che le parole che si vuole trasmettere facciano parte di un vocabolario V e che siano state codificate con delle stringhe di zeri ed uni. Per fare un esempio significativo, anche se troppo modesto per avere valore pratico, supponiamo che il nostro vocabolario abbia non piú di 16 parole e che, quindi, possano essere codificate con delle stringhe di lunghezza 4. Ad esempio la parola "algebra" = 0001, "giustizia" = 0101 ecc.

Il metodo che vogliamo esporre consiste nel codificare il modo diverso le parole di V in modo che esse corrispondano agli elementi del nucleo di una opportuna matrice. Se durante la trasmissione queste nuove stringhe si modificano di poco uscendo dal nucleo, riusciremo ugualmente riconoscerle e anche correggere l'errore.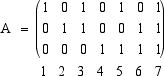
Consideriamo la matrice A

Notiamo che le colonne della matrice A rappresentano, nell'ordine, i numeri interi fino al 7 scritti in base due. (1 si scrive 001, 2 si scrive 010, 3 si scrive 011, poi 100, 101 ecc) La matrice A è, come si vede immediatamente, ridotta e il suo rango vale tre. Essa definisce quindi una applicazione lineare

il cui nucleo ha dimensione 4. Calcoliamo ora esplicitamente, con i metodi che abbiamo visto in precedenza e applicabili qualunque sia il campo degli scalari, una base per il Ker A. Possiamo scegliere come variabili libere la terza, la quinta la sesta e la settima. Risolvendo il sistema Ax=0 a ritroso troviamo:

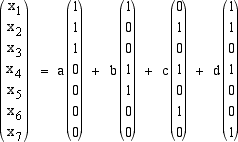Indicando rispettivamente con u₁ , u₂ , u₃ , u₄ i 4 vettori che abbiamo trovato, possiamo dire che ogni vettore x di Ker A si scrive in modo unico come loro combinazione lineare:

Utilizziamo questa base per codificare le parole del nostro vocabolario in stringhe di lunghezza 7 elementi. Ciò viene fatto identificando biunivocamente le parole con un vettore di Ker A: la parola abcd sarà identificata al vettore au₁ + bu₂ + cu₃ + du₄, così, ad esempio, la parola "giustizia" cioé 0101, sarà codificata col vettore u₂ + u₄ che risulta essere il vettore (che quì scriviamo per ragioni tipografiche come vettore riga) (0,1,0,0,1,0,1).
Supponiamo ora di trasmettere i vettori di F⁷ e supponiamo che il segnale venga disturbato durante la trasmissione. Facciamo l'ipotesi, fondamentale, che il rumore sia piccolo cioè che al più una sola componete delle 7 componenti che formano il segnale, possa modificarsi. In questa ipotesi siamo in grado di individuare la componente che si è modificata e riconoscere il segnle originale.
Sia abcd la parola da trasmettere, sia p = au₁ + bu₂ + cu₃ + du₄ il vettore di Ker A che codifica la parola e supponiamo che le sue componenti siano x₁, ... , x₇ sia p' il vettore colonna che riceviamo le cui 7 componenti siano x'₁, ... , x'₇. Il vettore p' è uguale a p tranne al più per una componente. Se è la prima componente a cambiare vuol dire che x₁ è diverso da x'₁ (ciò significa, ricordiamolo, che x'₁ = x₁+1) mentre le altre componenti sono uguali. In questo caso dunque p' = p + e₁ dove e₁ = (1,0,0,0,0,0,0) è il primo vettore della base canonica di F⁷. In generale abbiamo che, se a cambiare è la i-esima componente di p, allora

Ora, per identificale il rumore e ricostruire il segnale originario, basta calcolare Aq'. Abbiamo infatti

essendo c_i la i-esima colonna della matrive A che rappresenta il numero i (cioé la componente che si è modificata) scritto in base 2. Se dunque p' è la parola che riveviamo, calcolando il prodotto Ap' troviamo tre numeri (y₁,y₂,y₃) che mi dicono quale componete di p' devo cambiare per trovare il segnale originale p: la componente da cambiare è la componente

Supponiamo, ad esempio, che la parola da trasmettere sia "giustizia" cioè 0101, codificandola otteniamo il vettore di Ker A u₂ + u₄ cioè il vettore (colonna) p=(0,1,0,0,1,0,1). Supponiamo ora che il vettore che riceviamo, lievemente disturbato, sia il vettore p' = (0,1,1,0,1,0,1). Calcolando Ap' troviamo (1,1,0) da cui i = 1+2 = 3, e quindi è la terza componente di p' che va cambiata e il segmale originale, che non conoscevamo, è (0,1,0,0,1,0,1).

L'idea di Hamming consiste nel codificare le parole come vettori di una dato sottospazio (il Ker A) di uno spazio più grande facilmente riconoscibile algebricamente (p è una parola del codice se e solo se Ap=0). Le 8 fibre dell'applicazione lineare L_A

e_i + Ker A = { e_i + p: p Ker A}

corrispondono alle parole che hanno la i-esima (e solo quella) componente modificata.

Non è difficile generalizzare questo argomento per trattare vocabolari più grandi.
Fissiamo un numero intero n e consideriamo la matrice a coefficenti in F che ha per colonne le stringhe di lunghezza n che rappresentatno ordinatamente i numeri 1, 2, 3, 4, ... , 2ⁿ-1 = N scritti in base 2. La prima colonna sarà dunque il vettore (colonna) (1,0,0,..,0), la sconda colonna il vettore (0,1,0,0..,0), la terza colonna il vettore (1,1,0,0,..,0) ecc. Abbiamo in questo modo una matrice A di n righe e N colonne (nel caso che abbiamo trattato dettagliatamente avevamo n=3) che, si vede immediatamente, è ridotta e ha rango n. Tale matrice definisce una applicazione lineare di F^N in Fⁿ il cui nucleo ha dimensione N-n = M. Fissiamo una base u₁,u₂,...,u_M del nucleo di A e codifichiamo le parole del nostro vocabolario, che in questo potranno arrivare fino a 2^M, come vettori del nucleo: la parola a₁a₂...a_M si codifica col vettore p = a₁u₁ + a₂u₂ + ... + a_Mu_M. Se p' è la parola ricevuta e se p' è diversa da p solo per la i-esima componente, cioé se p' = p + e_i allora il prodotto Ap' fornisce, in base due, la componente da modificare per ricostruire p. Osserviamo che il numro 2^M di parole che possiamo codificare diventa molto grande anche per valori piccoli di n. Per n = 4 abbiamo N=15, M=11 e il vocabolario può contenere fino a 2¹¹=2048 parole. Per n=5 abbiamo M = 26 e 2²⁶ = 262.180.864. Naturalmente il prezzo che si paga nell'avere un modo per eliminare un piccolo rumore consiste in questo: che una stringa di lunghezza M (il messaggio originale) viene codificato come una striga di lunghezza N. Nell'esempio relativo al caso n=5 una striga di lunghezza 26 (con la quale possiamo elencare più di 200 milioni di parole) viene codificata e poi trasmessa come una stringa di lunghezza N = 31.