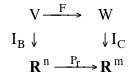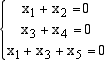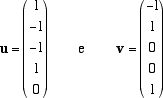|
Isomorfismi di spazi vettoriali
Un isomorfismo (iso=stesso, morfismo = forma) tra due spazi vettoriali è una trasformazione biunivoca che conserva la struttura di spazio vettoriale. Precisamente
Definizione
Dati due spazi vettoriali V e W su uno stesso campo K, diciamo che V è isomorfo a W se esiste una trasformazione lineare F: V ------> W biunivoca. La trasformazione lineare F è detta, in questo caso un isomorfismo di V in W.
Dato che F è lineare e biunivoca il solo vettore di V che si trasforma in 0 è il vettore nullo dunque Ker F = {0} e Im F = W.
La biunivocità della trasformazione F ci permette di definire la trasformazione inversa F-1 che associa a un vettore w si W l'unico vettore di u di V tale che F(u)=w. Non è difficile dimostrare che anche F-1 è una trasformazione lineare.
Gli isomorfismi a differenza dei morfismi, conservano l'indipendenza lineare e la dimensione. In altri termini abbiamo
Teorema
Sia F: V ------> W una trasformazione lineare di V in W. F è un isomorfismo se e solo se dim V = dim W e F trasforma vettori linearmente indipendenti in vettori linearmente indipendenti.
(Dimostrazione)
Come conseguenza di questo teorema abbiamo che un isomorfismo trasforma un sottospazio di U di V di dimensione k,
U = Span(v1, v2, ... , vk)
in un corrispondente sottospazio Z=F(U) di W della stessa dimensione k
Z = Span(F(v1), F(v2), ... , F(vk))
Un isomorfismo essendo una corrispondenza biunivoca tra due spazi vettoriali che conserva le operazioni vettoriali permette di trasferire da una spazio all'altro le operazioni, le proprietà, le caratteristiche dell'uno nelle corrispondenti operazioni proprietà , caratteristiche dell'altro. In questa direzione abbiamo il seguente teorema detto di rappresentazione perché permette di rappresentare isomorficamente ogni spazio vettoriale di dimensione n con lo spazio Kn dei vettori numerici.
Teorema (di rappresentazione)
Sia V uno spazio vettoriale su K di dimensione n. Esiste un isomorfismo (non canonico) di V con Kn.
Dimostrazione
Fissiamo una base B = {v1,v2, ... , vn} di V e consideriamo l'applicazione che associa al generico vettore
v = a1v1 + a2v2 + ... + anvn
il vettore numerico (a1, a2, ... , an) dato dalle sue componenti.
La definizione ha senso dal momento che, fissata la base, le n componenti (a1, a2, ... , an) del vettore v sono univocamente individualte.
Per come sono state definite le operazioni coi vettori numerici, si vede immediatamente che l'applicazione che abbiamo definito è lineare e che il suo nucleo è nullo dal momento che il solo vettore le cui componenti siano (0,0,...,0) è il vettore nullo. Essendo i due spazi della stessa dimensione questo implica che F è un isomorfismo. l'applicazione che abbiamo definito, spesso indicata con IB si scrive
IB(v) = I
B
(a1v1 + a2v2 + ... + anvn) = (a1, a2, ... , an)
Questo isomorfismo dipende strettamente dalla base scelta, cambiando base le componenti di uno stesso vettore cambiano e quindi cambia la n-upla che gli viene associata. Per questo l'isomorfismo è detto non canonico.
Notiamo anche che l'isomorfismo che abbiamo definito trasforma i vettori della base di V nei vettori della base canonica di Kn
Questo teorema ci permette di trasferire a livello numerico, cioè nello spazio Rn (o Kn), lo studio di uno spazio vettoriale qualsiasi e di una qualsiasi applicazione lineare. Per fare questo occorre fissare una base che permette di identificare un vettore con le sue componenti. Se prendiamo ad esempio lo spazio dei vettori geometrici e se i, j, k è una sua base abbiamo un isomorfismo tra questo spazio ed R3 che identifica il vettore ai+bj+ck con la terna ordinate (a,b,c). Occorre tuttavia tener presente che tale identificazione dipende strettamente dalla base scelta.
Nello stesso modo possiamo descrivere una applicazione lineare tra spazi vettoriali di dimensione finita con una matrice esattamente come si fa per descrivere le applicazione lineari L di
Rn in Rm. In quel caso la matrice che descrive l'applicazione lineare ha per colonne le componenti dei vettori L(ei) nella base canonica di Rm. Possiamo fare la stessa cosa in generale.
La differenza rispetto al caso precedente è che ora non abbiamo a disposizione una base, come
la base canonica, da cui partire. In generale uno spazio vettoriale ammette infinite basi e per poter descrivere con una matrice la applicazione lineare occorre,
innanzi tutto, scegliene una per il dominio e una per il codominio. Questa scelta il più delle volte non è univoca e può essere fatta in modi diversi. Per questo, in generale,
parliamo di matrice associata a una data applicazione lineare rispetto a due basi fissate, una di V e l'altra di W, cambiando le basi, cambia la matrice.
Sia dunque dim V = n , B = {v1,
v2, ... , vn} una base di V, dim W = m , C = {w1,
w2, ... , wm} una base di W e sia F una data applicazione lineare di V in W. A partire da questi dati possiamo
costruire, come nel caso di vettori numerici, una matrice che rappresenti la trasformazione F. Tale matrice ha m righe (quanto è la dimensione di W)
e n colonne (quanto è la dimensione di V), si chiama la matrice associata a F nelle basi B
e C e viene indicata col simbolo MC,B(F) per
evidenziare la sua dipendenza dalle basi scelte. Attenzione all'ordine col quale sono indicate le due basi: a sinistra la base del codominio e a destra quella del
dominio. Le colonne di questa matrice si costruiscono come nel caso precedente:
- si prende il primo vettore v1 della base B di V
- si trasforma il vettore v1 con la trsformazione lineare F
- si esprime il vettore F(v1) come combinazione lineare dei vettori della base C di W
F(v1) = a1,1w1 + a2,1w2 + ... + am,1wm
- i coefficienti a1,1 , a2,1 , ... , am,1 , così calcolati vengono scritti nella prima colonna della matrice
MC,B(F)
- si itera il procedimento per gli altri vettori v2, ... , vn della base
B costruendo nello stesso modo le altre colonne della matrice.
La matrice che abbiamo costruito descrive esattamente la applicazione lineare F nel senso che il generico vettore v di V viene trasformato da F nel
vettore w = F(v) di W le cui componenti nella base C si ottengono moltiplicando per
MC,B(F)
le componenti di v nella base B. In altri termini se
v = x1v1 + x2v2 + ... + xnvn
allora
F(v) = y1w1 + y2w2 + ... + ymwm
dove, indicando con A = MC,B la matrice che abbiamo descritto, con x e con y i vettori colonna le cui componenti sono xi (i=1,2,...,n) e yj, il vettore colonna y è dato da
(j=1,2,...,m),
y = A . x
Possiamo scrivere questo in modo più concettuale e conciso facendo intervenire il concetto di isomorfismo e il teorema di rappresentazione. La matrice A = MC,B definisce l'applicazione lineare LA tra gli spazi di vettori numerici Rn e Rm isomorfi a V e W rispettivamente la quale, tramite le basi, rappresenta l'applicazione lineare F di partenza. Queste due trasformazioni lineari sono essenzialmente le stesse, in modo che per studiare F, possiamo usare A, che la rappresenta isomorficamente, e che, essendo una matrice numerica può essere trattata in modo algoritmico. Il seguente diagramma sintetizza questo complicata rappresentazione di una applicazione lineare
Se prendiamo un qualunque vettore v di V e lo trsformiamo prima con F e poi con IC troviamo lo stesso vettore di Km ottenuto trasformandolo prima con IB e poi con LA. Infatti se v è un generico vettore di V, IB(v)=x dove x è il vettore formato dalle componenti di v nella base B. Applicando ora LA abbiamo
LA(IB(v))=LA(x)=A.x
Se seguiamo l'altro percorso abbiamo dobbiamo prima calcolare F(v) e poi trovare le componenti y di F(v) nella base C:
IC(F(v))=y
La condizione
LA o IB =
IC o F
che si legge dicendo che il diagramma è commutativo, esprime sinteticamente quello che abbiamo detto prima e cioè che y = A.x
Osserviamo che l'immagine di F è un sottospazio di W che si trasforma tramite IC , per ragioni insiemistiche, nell'immagine di LA e questi due sottospazi, essendo IC un isomorfismo, sono isomorfi. Ne segue, dato che l'immagine di LA è generata dalle colonne di A, che
dim Im F = rango (A)
dato che il rango di A è il massimo numero di colonne linearmente indipendenti. Di conseguenza, per il teorema di struttura,
dim Ker F =n - rango (A)
e il calcolo del nucleo di F si esegue calcolando le soluzioni del sistema omogeneo Ax = 0 e trasferendo, con l'isomorfismo inverso di IB, le soluzioni in V. Ugualmente il calcolo delle fibre F-1(w) si esegue risolvendo il sistema lineare non omogeneo A.x=b (b è formato dalle componenti di w nella base C) e trasferendo, come per il nucleo, con l'isomorfismo inverso di IB, le soluzioni in V.
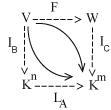
In questo modo abbiamo visto come, lavorando con la matrice A associata all'applicazione lineare F, sia possibile calcolare il nucleo, l'immagine e le fibre di F. La cosa interessante è che la matrice A dipende dalla scelta delle due basi e scegliendo opportunamente la basi può essere più o meno complicata. In questo ordine di idee, come abbiamo rappresentato un qualunque spazio vettoriale di dimensione finita con uno spazio di vettori numerici, nello stesso modo possiamo rappresentare ogni applicazione lineare con una proiezione. Una proiezione di Rn in Rm è una applicazione
Pr : Rn ------> Rm
F((x1,x2,...,xn)) =(x1,x2,...,xr,0,...,0)
dove 0 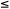 r r 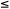 m m
è anche inteso che r 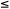 n e che il numero degli zeri è m-r. Tale trasformazione proeitta il vettore numerico (x1,x2,...,xn) sulle sue prime h componenti. Il teorema sulla rappresentazione delle applicazioni lineari afferma che ogni applicazione lineare si può rappresentare con una proiezione. Precisamente n e che il numero degli zeri è m-r. Tale trasformazione proeitta il vettore numerico (x1,x2,...,xn) sulle sue prime h componenti. Il teorema sulla rappresentazione delle applicazioni lineari afferma che ogni applicazione lineare si può rappresentare con una proiezione. Precisamente
Teorema (di rappreswentazione per le applicazione lineari)
Sia F : V ------> W una applicazione lineare tra spazi vettoriali su R di dimensione finita. E sia n= dim V, m= dim W e r= dim Im F. Esiste allora una base B di V e una base C di W tale che
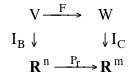
il diagramma è commutativo.
Ciò significa che, a patto di scegliere opportunamente le basi per rappresentare con una matrice il morfismo, possiamo sempre supporre che il morfismo sia una proiezione. Questo giustifica le 4 immagini con le quali abbiamo descritto i possibili morfismi tra spazi vettoriali:
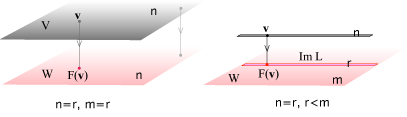
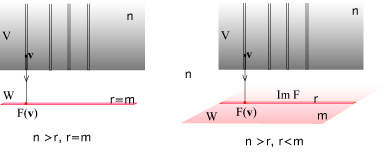
I tre numeri interi, n,m,r indicano le dimensioni dei diversi spazi e queste sono le possibili situazioni, essenzialmente diverse tra loro, che possono presentarsi. Esse sono determinate dai possibili valori n,m,r il cui calcolo è essenzialmente ridotto all'algoritmo di Gauss. Scegliere le basi è come scegliere un determinato punto di vista dal quale "guardare" il dato morfismo F, cambiando basi cambia, anche drasticamente, la matrice che descrive F ma non cambiano alcune proiprietà strutturali del morfismo stesso, come il rango,il determinate (quando esiste) ed altre ancora. Esiste una sorta di relativismo che consiste nel fatto che per descrivere un morfismo dobbiamo scegliere un dato modo di rappresentarlo scegliendo le basi, ogni scelta, ogni punto di vista, è legittimo, ma la descrizione che ne esce è relativa al punto di vista, punto di vista che può nascondere o illuminare le caratteristiche del morfismo che stiamo guardando.
La dimostrazione del teorema si ottiene scegliendo le basi come si erano scelte nella dimostrazione del teorema di struttura. La base C ={w1,w2,...,wr, wr+1,...,wm} è ottenuta prendendo una base di r vettori per l'immagine di F e prolungando tale base fino ad arrivare a una base di Rm. La base C ={v1,v2,...,vr, u1,...,un-r} è ottenuta prendendo una base u1,...,un-r del nucleo di F e scegliendo r vettori v1,v2,...,vr rispettivamente nelle fibre di w1,w2,...,wr. Calcoliamo la matrice A = MC,B(F) associata ad F in queste basi. Abbiamo F(v1)=w1 e quindi la prima colonna ha 1 sulla prima riga e 0 sulle altre.
F(v2)=w2 e quindi la seconda colonna ha 0 sulla prima riga 1 sulla seconda e 0 sulle altre. Analogamente si calcolano le prime r colonne. Le altre colonne sono tutte nulle dato che F(ui)=0. La matrice A è dunque la matrice a blocchi
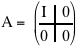
il cui primo blocco è la matrice identica di ordine r, e gli altri sono nulli: abbiamo cioè m-r righe nulle e n-r colonne nulle. Il generico vettore x=(x1,x2, ... , xn) si trasforma in A.x=(x1,x2, ... , xr,0,...,0) e quindi il morfismo LA è proprio la proiezione Pr.
Usando questo quadro concettuale è facile vedere come alla composizione di trasformazioni lineari corrisponda "isomorficamente" il prodotto di matrici.
Siano V, W e Z tre spazi vettoriali di dimensione finita su un campo K
e siano date le trasformazioni lineari
F: V------> W e G : W------> Z
Supponiamo anche di aver scelto, per ogni spazio vettoriale, una base:
sia
B una
base di V
C
una base di W e
D
una base di Z .
A partire da queste basi possiamo calcolare le matrici
A = MC,B(F),
B = MD,C(G) ,
C = MD,B(GoF)
Consideriamo il seguente diagramma
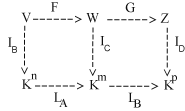
Dato che i due diagrammi quadrati sono commutativi, qualunque sia il percorso scelto per andare da V a Kp si ottiene la stessa cosa. In particolare il j-esimo vettore vj della base B di V si trasforma tramite F in F(vj) il quale si trasforma, tramite IC nella j-esima colonna della matrice A. Sia aj tale colonna. Se trasformiamo ora aj con LB troviamo B. aj che è la j-esima colonna della matrice A.B. Seguiamo ora un percorso diverso: trasformiamo come prima vj in F(vj), poi trasformiamo questo vettore con G, troviamo G(F( vj))=(GoF)(vj) e infine trasformiamo il risultato che abbiamo trovato con
ID. Il risultato di tutto questo è la j-esima colonna della matrice C = MD,B(GoF). Essendo il digramma comutativo queste due colonne coincidono e quindi, avendo le matrici B.A e C le stesse colonne, sono uguali. Ciò dimostra che
MD,B(GoF) =
MD,C(G) . MC,B(F)
Queste considerazioni ci consentono di trovare facilmente le formule che regolano il modo in cui cambiano le componeti di un vettore cambiano la base e anche come cambia la matrice associata a una trasformazione lineare cambiando le basi.
Consideriamo una spazio vettoriale V di dimensione n e sia B = {v1,v2, ... , vn} una sua base. Un generico vettore v di V si scrive univocamente
v = x1v1+x2v2+ ... + xnvn
e le sue componenti x= (x1,x2,...,xn) scritte come colonna, danno luogo all'immagine di v tramite IB.
Consideriamo ora una seconda base di F, sia questa B' = {v'1,v'2, ... , v'n}. Lo stesso vettore v di V che avevamo considerato prima si scrive ora come combinazione lineare dei vettori della nuova base come
v' = x'1v'1+x'2v'2+ ... + x'nv'n
e le sue componeti x' =(x'1,x'2,...,x'n) scritte come colonna,danno luogo all'immagine di v tramite IB'; cerchiamo la relazione che lega il vettore numerico a n componenti x = IB(v) al vettore numerico a n componenti x' = IB'(v). Per questo consideriamo il diagramma commutativo
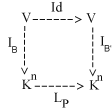
dove Id(v) = v è la trasformazione identica. La matrice P che risulta da questo diagramma è la matrice MB',B(Id), matrice che si chiama matrice del cambiamento di base. Ricordiamo che questa matrice ha come j-esima colonna le componenti del
vettore vj nella nuova base B'. Osserviamo che, dato che P è la matrice associata a un isomorfismo, è una matrice invertibile. La sua inversa P-1 è la matrice che esprime le componenti x di v nella base B in funzione delle componenti x' di v nella base B':
x' = P. x e x = P-1. x'
dove P = MB',B(Id) è la matrice che ha per colonne le componenti dei vettori della prima base B scritti come combinazioni lineari dei vettori della seconda base B'.
In modo del tutto analogo possiamo trovare le formule che regolano il cambiamento della matrice associata a una trasformazione lineare quando si cambiano le basi. Consideriamo a titolo di esempio il caso più frequente che è quello in cui F è un endomorfismo, cioé una trasformazione lineare di V in se stesso. Scegliamo una base B di V e scriviamo la matrice associata a F usando sia per il dominio che per il codominio la stessa base B. Sia A= MB,B(F). Prendiamo ora una seconda base B' di V e scriviamo, come prima, la matrice associata a F in questa nuova base. Sia B= MB',B' (F) questa nuova matrice. Vogliamo trovare la relazione che lega A con B. Per questo consideriamo il diagramma commutativo
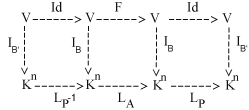
La commutatività del diagramma implica che
B = P . A . P-1
dove P è la matrice del cambiamento di base MB',B (Id). La formula che abbiamo trovato descrive esattamente il legame tra le due matrici.
Notiamo che le due matrici A e B, che si dicono coniugate quando esiste una matrice P invertibile tale che
B = P . A . P-1, rappresentano la stessa trasformazione lineare in due basi diverse: esse sono, pur essendo molto diverse tra loro, in un certo senso "isomorfe". Ad esempio hanno lo stesso rango perché il rango, essendo la dimensione dell'immagine di F, dipende solo da F e non dal modo come la si rappresenta. Con una metafora, possiamo dire che la trasformazione lineare F può essere vista in tanti modi diversi a seconda della scelta del punto di vista dal quale la guardiamo. La scelta del punto di vista corrisponde alla scelta di una base che ci permette di descrivere concretamente la trasformazione tramite una matrice numerica. Questa matrice peró cambia cambiando base. In questo modo abbiamo infinite rappresentazioni della stessa trasformazione lineare le quali hanno in comune le proprietà intrinseche della trasformazione, le proprietà cioé che non dipendono dalla scelta di una base, come, ad esempio il rango. Le proprietà di una matrice quadrata A che che si ritrovano in ogni altra matrice coniguata ad A si chiamano proprietà invarianti della matrice. Un'altra proprietà invariante, oltre al rango, è il determinate. Risulta infatti, per il teorema di Binet,
det(B) = det(P . A . P-1) = det(P) det(A) det( P-1) =
[det(P) det( P)-1] det(A) = det(A)
cambiando dunque punto di vista il modo in cui vediamo la trsformazione cambia, ma il determinate resta sempre lo stesso.
Esempio
Consideriamo lo spazio vettoriale

e sia L l'applicazione lineare di V in V che trasforma il vettore (x1,x2,x3,x4,x5) nel vettore
(x3,x4,x1,x2,x5). Vogliamo innanzi tutto trovare una base B
di V e poi la matrice MB,B associata a L in tale base. Si vede facilmente, risolvendo il sistema
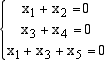
che dim V = 2 e che una sua base è formata dai vettori
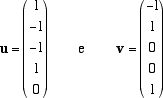
Dunque V = Span(u,v) e possiamo scegliere come base di V la base B =
{u,v}. La matrice che cerchiamo è dunque una matrice 2x2 e le sue colonne si calcolano trasformando con L i vettori
u e v e scrivendo il risultato come combinazione lineare di u e v. Poichè L((x1,x2,
x3,x4,x5)) =
(x3,x4,x1,x2,x5), abbiamo L((1,-1,-1,1,0)) = (-1,1,1,-1,0) e
L((-1,1,0,0,1))= (0,0,-1,1,1) e dunque
L(u) = -u
L(v) = u + v
e quindi la matrice associata a L nella base u e v è
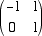
Osserviamo che se w è il vettore colonna che ha come componenti (0,0,-1,1,1) anche i vettori v e w
formano una base si V e, chiamando C = {v , w} questa secona base, possiamo calcolare,
per esercizio,
le matrici MC,B, MC,C,
MC,B. Poichè
L(u) = v - w
L(v) = w
la matrice associata MC,B è
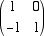
Analogamente le matrici MC,C e MB,C
sono, rispettivamente
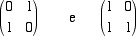
Osserviamo che la matrice MB,C è la matrice inversa della matrice
MC,B e che la matrice MC,C sembra
più semplice delle altre.
In conclusione una stessa applicazione lineare può rappresentarsi con diverse matrici a seconda di come vengono scelte le basi.
|
|