Lezioni di Geometria

Franco Ghione


Capitolo III



III.1 Somma di vettori geometrici

Dati due vettori geometrici u e v la loro somma u+v si calcola nel seguente modo:

  • si sceglie un qualunque punto A dello spazio
  • si applica in A il vettore u e si trova il segmento orientato AB
  • si applica in B il vettore v e si trova il segmento orientato BC
  • Il segmento orientato AC ottenuto "sommando i due cammini" rappresenta un vettore che, per definizione è la somma di u e v.

Notiamo che, dato A, la costruzione non è ambigua essendo unico, per la proprietà 1 il segmento AB che rappresenta u e quindi il segmento BC che rappresenta v. È facile anche rendersi conto che se si cambia posizione del punto A e si eseguono le operazioni che abbiamo descritte a partire da un'altro punto A' dello spazio il risultato che otteniamo è un altro segmento orientato A'C' che risulta equipollente ad AC.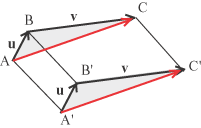


Per convincersi di questo basterà dimostrare che il segmento orientato A'C' è uguale e parallelo ad AC, cioé che la figura AA'C'C è un parallelogramma1. La costruzione precedente del vettore somma può esprimersi con la formula

AB + BC = AC

Osserviamo ancora che il risultato della somma, pur essendo costruito a partire da dei segmenti dipende solo dalla direzione, dal verso e dal modulo dei due vettori che essi rappresentano. La figura animata seguente permette di modificare la direzione, il verso ed il modulo di due vettori u e v e di calcolare automaticamente la loro somma u+v. Cambiando la posizione di A il risultato è sempre un segmento orientato equipollente ad AC.

Figura animata

È molto utile per fissare delle corrette immagini mentali modificare più volte la figura animata per rendersi ben conto di come si possa sommare una direzione un verso e un modulo con un'altra direzione, un'altro verso e un'altro modulo. In particolare è utile, usando la figura animata del testo fare la somma di vettori con la stessa direzione e lo stesso verso, o con la stessa direzione e versi opposti o anche fare la somma di due vettori uguali.
L'operazione di invertire il verso di un segmento orientato da luogo a una importante operazione tra i vettori che permette, dato un qualunque vettore u, di costruire un vettore opposto -u. Se rappresentiamo u col segmento orientato AB, cioè se u = AB allora, per definizione -u = BA. Risulta ovviamente che

u + (-u) = 0

dato che AB + BA = AA = 0.

L'operazione di somma che abbiamo introdotto verifica importanti proprietà che ci permettono, entro certi limiti, di trattare i vettori come se fossero numeri. Questa attitudine della matematica di creare delle analogie formali tra strutture diverse permette di trasferire metodi e concetti da casi semplici e ben noti a situazioni diverse e, generalmente, più complesse. Questo processo analogico diventa rigoroso solo se, nel corso dei propri ragionamenti, si usano, nel nuovo contesto, le stesse proprietà formali con le quali procediamo nel corso di una dimostrazione nel contesto usuale. La somma tra vettori geometrici è per molti versi simile alla ordinaria somma tra numeri.


III. 2 Proprietà della somma di vettori geometrici

  • (u + v) + w = u + (v + w)     proprietà associativa
  • u + v = v + u      proprietà commutativa
  • u + 0 = u      esistenza dello zero
  • u + (-u) = 0     esistenza dell'opposto
Naturalmente queste proprietà valgono qualunque siano i vettori geometrici u, v, w scelti.

La dimostrazione di queste proprietà non crea particolari problemi.
Per dimostrare la proprietà associativa basta osservare che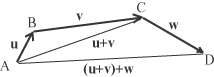


(u + v) + w = (AB + BC) + CD = AC + CD = AD

D'altro canto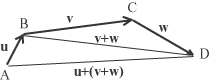



u + (v + w) = AB + (BC + CD) = AB + BD = AD

La proprietà commutativa ci riporta alla così detta regola del parallelogramma dalla quale probabilmente ha avuto origine, con Leonardo da Vinci, l'algebra dei vettori.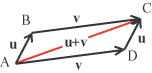

Abbiamo infatti che AB + BC = AD + DC dato che, essendo AB equipollente a DC e AD equipollente a BC, la figura che si ottiene è un parallelogramma la diagonale del quale rappresenta il vettore somma.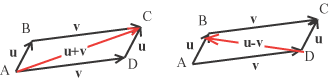
Per analogia con l'aritmetica ordinaria e per semplificare la notazione la differenza tra due vettori geometrici sarà indicata con u - v indicando con questo il vettore u + (-v). Osserviamo che, se u e v sono applicati nello stesso punto A allora il vettore somma e il vettore differenza sono rappresentati dalle due diagonali del parallelogramma generato da quei vettori. Nel caso della differenza si deve fare attenzione a non confondere u - v con v - u che sono rappresentati entrambi con la diagonale DB del parallelogramma ma con versi opposti. Applicando i vettori in D si vede subito che DB = u - v e non BD.



III. 3 Prodotto di un vettore geometrico per uno scalare

La somma di n vettori uguali a v si indica con nv.

v + v + v + ... + v = nv

Mentre la m'esima parte di v è quel vettore che ha la stessa direzione e verso di v ma lunghezza un m-esimo di quella di v. Tale vettore è denotato con (1/m)v. Se si somma n volte il vettore (1/m)v otteniamo il vettore (n/m)v che ha la stessa direzione, lo stesso verso di v ma il modulo (n/m) volte quello di v. Più in generale dato un numero reale a positivo o negativo e un vettore v è possibile definire un nuovo vettore denotato con av che si chiama il prodotto di v secondo lo scalare a o anche il multiplo di v secondo lo scalare a. Il nuovo vettore av ha la stessa direzione di v, lo stesso verso se a > 0, il verso opposto se a < 0 e il modulo uguale al modulo di v moltiplicato per il valore assoluto o modulo di a 2 . In una formula il modulo di av è

|av| = |a||v|

L'esistenza del vettore geometrico av è garantita dal così detto assioma di continuità3 che viene generalmente trattato in tutti i suoi significati nei corsi di logica matematica.

Dalla definizione di prodotto di un numero per uno scalare, segue che

0v = 0 , 1v = v , (-1)v = -v

È interessante notare come la moltiplicazione di un vettore geometrico per -1 ne cambi il verso lasciando inalterata direzione e modulo. Ne segue che, se moltiplichiamo un dato vettore geometrico due volte per -1, otteniamo il vettore di partenza. Dunque, in questo contesto geometrico, la regola dei segni si interpreta dicendo che cambiando due volte il verso di percorrenza di una retta si ottiene il verso di partenza. Il prodotto di un vettore geometrico per uno scalare ha alcune importanti proprietà algebriche che ci permettono di operare coi vettori geometrici come si opera coi numeri nell'aritmetica elementare.

  • a(bv) = (ab)v
  • (a+b)v = av + bv
  • a(v + w) = av + aw

    • La prima proprietà deriva facilmente dalla definizione. Se a o b è nullo la cosa è ovvia, in caso contrario abbiamo quattro casi possibili da analizzare uno a uno : a>0 e b>0, a>0 e b<0, a<0 e b>0, a<0 e b<0. A titolo d'esempio trattiamo il caso a>0 e b<0. Il vettore bv ha la stessa direzione di v, verso opposto (perché b è negativo) e modulo |b||v|. Il vettore a(bv) ha la stessa direzione di bv, verso uguale a quello di bv (perch´ a è positivo) e modulo |a|(|b||v|)= |a||b||v|. D'altra parte il vettore (ab)v ha la stessa direzione di v, verso oposto (perché ab è negativo) e modulo uguale a |ab||v|. Poiché |ab| = |a||b|, la formula risulta dimostratrata.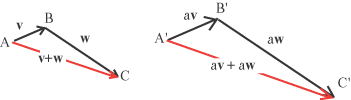

    Anche per la seconda formula dobbiamo tenere conto dei segni di a e b e a+b. Vediamo il caso in cui a>0 e b>0. In questo caso av è il vettore che ha direzione e verso di v e il modulo uguale a a|v|, analogamente il vettore bv ha stessa direzione stesso verso di v e modulo uguale a b|v|. Sommiamo ora questi due vettori geometrici. Sia A un qualunque punto dello spazio e av=AB e bv=BC. Poichè i vettori hanno la stessa direzione i punti A, B, C sono allineati e dunque la lunghezza del segmento AC è uguale alla somma delle lunghezze di AB e BC, quindi |av + bv| = |av| + |bv| = |a||v| + |b||v| = (|a|+|b|)|v|, ma, essendo a e b positivi, quest'ultima quantità vale |a+b||v|. Da questo segue che i vettori geometrici av + bv e (a+b)v sono uguali avendo la stessa direzione (quella di v), lo stesso verso (quello di v) e lo stesso modulo.

    Più interessante è la dimostrazione della terza formula che segue dalla teoria euclidea della similitudine (Euclide , Elementi, Libro VI). Supponiamo che a sia positivo. Nel caso opposto si procederà analogamente. Fissiamo un punto A dello spazio e sia v=AB e w = BC. Il vettore v + w sarà quindi rappresentato dal segmento AC.

    Fissiamo ora un'altro punto A' dello spazio e sia av=A'B' e aw = B'C'. Il vettore av + aw sarà quindi rappresentato dal segmento A'C'. Poiché |av| = a|v| e |aw|=a|w|, essendo questi moduli le lunghezze dei segmenti A'B' e B'C', abbiamo che il rapporto tra AB : A'B' = BC : B'C' = a. Inoltre l'angolo ABC e l'angolo A'B'C' sono uguali. Infatti abbiamo che AB e A'B' sono paralleli avendo i vettori geometrici AB = v e A'B' = av la stessa direzione e analogamente sono paralleli BC e B'C'. I triangoli ABC e A'B'C' hanno un angolo uguale e i lati che comprendono quest'angolo nella medesima proporzione, ne segue ( Euclide VI, 4) che i due triangoli sono simili e quindi A'C' è parallelo ad AC, ha dunque la stessa direzione e lo stesso verso, inoltre la sua lunghezza è a volte quella di AC. Ne segue che av + aw = a(v + w).

    Dati due o più vettori geometrici, u, v, ... ,w, una combinazione lineare dei vettori u, v, ... ,w è una espressione del tipo

    au + bv + ... + cw

    Gli scalari a, b, ... , c sono detti coeffcienti della combinazione lineare. Con una immagine legata alla statica, scienza dalla quale questi concetti hanno tratto origine, si dice anche che i vettori u, v, ... ,w sono stati presi con i pesi a, b, ... , c e sommati tra loro.

    Cliccando sulla figura si apre una pagina animata che aiuta ad esercitarsi sul calcolo di combinazioni lineari di vettori. In fondo alla pagina sono proposti degli esercizi pratici da realizzare servendosi della figura animata. Questa pratica aiuta a svolgere correttamente e con facilità gli esercizi che proponiamo in fondo a questa sezione.

    III. 4 Il centro di una configurazione finita di punti

    Le idee che ora esponiamo si devono a Hermann Gunter Grassmann (1809-1877) la cui opera fondamentale (l'Ausdehnungslehre che significa teoria dell'estensione ) nella quale si introduce l'algebra vettoriale a n dimensioni, fu poco capita dai contemporanei tanto che alla fine Grassmann spostó i suoi interessi verso altre discipline come la botanica, la linguistica, le lingue orientali.
    Cominciamo a studiare un caso molto semplice: consideriamo due punti A1, A2 dello spazio e cerchiamo se esiste un punto ugualmente posizionato rispetto ad A1 e A2, punto che chiameremo il centro della configurazione A1, A2 . E' facile, in questo caso trovare, questo centro considerando il segmento A1 A2 e prendendo il punto medio C di tale segmento. Dal punto di vista vettoriale ciò significa che

    CA1 = A2C =- CA2

    cioé
    CA1 + CA2 = 0

    La cosa interessante è che questo punto C è il centro di qualunque parallelogramma che abbia A1 e A2 come vertici opposti. Ricordiamo che in ogni parallelogramma le due diagonali si incontrano nel loro punto medio, ciò significa, in termini vettoriali, che per ogni punto R dello spazio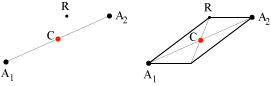

    RA1 + RA2 = 2RC

    Questa relazione, che deriva dalle proprietà geometriche dei parallelogrammi, può essere dimostrata facilmente usando il calcolo vettoriale con le sue proprietà. Possiamo infatti scrivere, per ogni punto R dello spazio

    CA1 + CA2 = (CR+ RA1) + (CR+ RA2)= 2CR + (RA1 + RA2)

    e quindi se C è il centro della configurazione cioé se CA1 + CA2 = 0 abbiamo, usando le proprietà che abbiamo visto e, in particolare l'esistenza dello zero e dell'opposto

    2CR + RA1 + RA2 = 0
    RA1 + RA2 + 2CR + (-2CR) = -2CR
    RA1 + RA2 + 0 = -2CR
    RA1 + RA2 = 2RC

    Come possiamo definire il centro di una configurazione formata da tre punti? L'idea di costruire il cerchio che passa per questi tre punti e prendere come centro della configurazione il centro di questo cerchio, come qualche studente ha suggerito, non è buona. Infatti se il triangolo che ha come vertici questi punti fosse un triangolo rettangolo, allora il centro si troverebbe su un lato (l'ipotenusa) cosa che non torna con l'idea che abbiamo di centro; inoltre, questa proposta diventa impraticabile per 4 o più punti dato che, in generale, quattro punti non stanno su una stessa circonferenza.
    Se vogliamo sviluppare una teoria generale valida anche per migliaia di punti dobbiamo trovare un'altra strada. Per questo il calcolo vettoriale riesce molto utile. Possiamo infatti dare la seguente generalissima definizione

    Definizione
    Si chiama centro di una configurazione di n punti A1, A2, ..., An un punto C dello spazio tale che

    CA1 + CA2 + ... + CAn = 0

    Si tratta ora di fare due cose: la prima è dimostrare che tale punto esiste ed è unico, la secoda è dare un algoritmo per costruire effettivamente tale punto.
    Il seguente teorema, la cui dimostrazione ricalca sostanzialmente il calcolo che abbiamo fatto prima, risolve entrambi i problemi.

    Teorema (H. Grassmann 1844)
    Dati n punti dello spazio A1, A2, ..., An se esiste un punto C tale che

    CA1 + CA2 + ... + CAn = 0
    allora per ogni punto R risulta
    RA1 + RA2 + ... + RAn = nRC

    Viceversa se esiste un punto C e un punto R tale che RA1 + RA2 + ... + RAn = nRC allora CA1 + CA2 + ... + CAn = 0.

    La dimostrazione si basa, come prima, sul fatto, alla base della definizione di somma tra vettori geometrici, che, comunque si scelga un punto R dello spazio, risulta

    CR + RA = CA

    Supponiamo dunque che esista un punto C tale che CA1 + CA2 + ... + CAn = 0, usando la proprietà che abbiamo ricordato, questa identità di vettori implica che CA1 + CA2 + ... + CAn = (CR+RA1) + (CR+RA2) + ... + (CR+RAn) =nCR + RA1 + RA2 + ... + RAn. Ma questo vettore è il vettore nullo e quindi RA1 + RA2 + ... + RAn = -nCR= nRC. Il viceversa si dimostra usando lo stesso calcolo.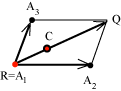

    Questo teorema implica che esiste almeno un punto C tale che CA1 + CA2 + ... + CAn = 0 : per trovarlo basta scegliere un punto R, calcolare il vettore RA1 + RA2 + ... + RAn = RQ, dividere il segmento RQ che si ottiene in n parti uguali e prendere su quel segmento il punto C in modo che il vettore nRC =RQ.
    Il teorema di Grassmann permette anche di dimostrare che esiste un unico punto C che verifica la condizione CA1 + CA2 + ... + CAn = 0, se infatti esistesse un secondo punto C' tale che C'A1 + C'A2 + ... + C'An = 0, allora applicando il teorema di Grassmann con R = C' avremmo 0 = C'A1 + C'A2 + ... + C'An = nC'C. Da cui ricaviamo C'C= 0 cioè C=C'. Dunque dati gli n punti A1, A2, ..., An il punto C che si costruisce con la procedura descritta non dipende dal punto R che si sceglie per partire: qualunque sia il punto scelto si trova sempre il punto C.

    Vediamo ad esempio come trovare il centro di tre punti A1, A2, A3. Scegliamo R=A1. Il vettore RQ = RA1 + RA2 + RA3 = A1A1 + A1A2 + A1A3 = A1A2 + A1A3.

    Dunque il centro C dei tre punti si trova costruendo il parallelogramma che ha come lati adiacenti i segmenti A1A2 e A1A3 e dividendo la diagonale in tre parti uguali come in figura.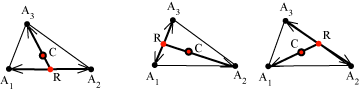
    Potevamo anche prendere come punto R il punto medio del segmento A1A2. In questo caso RA1 + RA2 = 0 e quindi RQ = RA1 + RA2 + RA3 =RA3 e C si trova dividendo questa mediana in tre parti uguali e prendendone (dalla parte di R) un terzo.

    Ma avremmo potuto scegliere come punto R il punto medio del segmento A1A3 o anche del segmento A3A2: il risultato, vista l'unicità del centro, sarebbe stato comunque lo stesso punto C. Da questo ricaviamo che le tre mediane di un triangolo si incontrano in un punto che divide ciascuna mediana nello stesso rapporto 1:2.

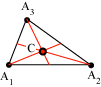    La nozione di centro si può generalizzare al caso di n punti pesati. Un punto pesato è una coppia (A,p) dove A è un punto dello spazio e p un numero reale. Dati n punti pesati (A1,p1) , (A2,p2) ,..., (An,pn) il loro centro è un punto C tale che

    p1CA1 + p2CA2 + ... + pnCAn = 0

    Gli argomenti e i calcoli che abbiamo fatto prima possono ora generalizzarsi a questa situazione. In particolare abbiamo che, se la somma dei pesi è non nulla, la condizione precedente vale se e solo se, per ogni punto R dello spazio risulta

    p1RA1 + p2RA2 + ... + pnRAn =(p1 + p2 + ... + pn)RC

    Quando la somma dei pesi è nulla Grassman azzarda l'idea che il centro si trovi all'infinito nella direzione del vettore a primo membro.
    Nel caso di due punti pesati (A,p) e (B,q) con pesi positivi il loro centro è un punto C del segmento AB tale che

    pCA+qCB = 0

    questo punto è il baricentro della bilancia data dal peso p applicato in A e dal peso q applicato in B dato che, la relazione precedente implica che AC=(q/p)CB e quindi, passando ai moduli

    |AC| : |CB| = q : p

    che è appunto la relazione che individua il baricentro del sistema dato dai due pesi.

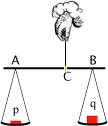
    Usando questo fatto (vedi esercizio 9) Grasmmann poteva dimostrare che il centro di n punti pesati corrisponde al baricentro del sistema fisico dato da quei punti con quei pesi ottenendo, in questo modo, una prima importante applicazione fisica della sua nuova algebra dei vettori che permetteva il calcolo del baricentro in forma intrinseca senza usare coordinate e sistemi di riferimento.

    Esercizi