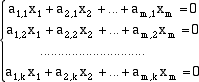Un modo per costruire sistemi di vettori linearmente indipendenti si basa sul seguente

Teorema VIII 1
Se u₁, u₂, ... , u_k sono vettori linearmente indipendenti e se u non è loro combinazione lineare,allora i k+1 vettori u₁, u₂, ... , u_k, u sono linearmente indipendenti.
(dimostrazione)

Per trovare un sistema di vettori linearmente indipendenti si parte, se esiste, da un vettore non nullo u₁ , che essendo non nullo sarà linearmente indipendente. Si descrivono i multipli di u₁ e si va a vedere se esiste un vettore che non sia multiplo di u₁. Se esiste ne scegliamo uno, sia esso u₂. Per il teorema precedente, i vettori u₁, u₂ sono linearmente indipendenti. Si descrivono ora tutte le combinazioni lineari dei vettori u₁, u₂ e si va a vedere se esiste un vettore u₃ che non sia loro combinazione lineare. Se esiste, i vettori u₁, u₂ e u₃ sono linearmnete indipendenti e possiamo preseguire il procedimento. Se dopo un numero finito di passi troviamo che ogni altro vettore dipende linearmente da quelli trovati abbiamo costruito quello che si chiama una base dello spazio vettoriale V. Più precisamente

Definizione
Diciamo che un sistema di vettori B = {u₁, u₂, ... , u_n} è una base di V se

• Span(u₁, u₂, ... , u_n) = V
• u₁, u₂, ... , u_n sono linearmente indipendenti

Per dimostrare che i vettori v sono linearmente dipendenti dobbiamo poter trovare una loro combinazione lineare nulla non banale, dobbiamo cioè poter trovare m scalari non tutti nulli tali che

Sostituiamo in questa relazione i vettori v con le loro espressioni come combinazioni lineari dei vettori u. Troviamo

espressione questa che, distribuendo la somma e raccogliendo i coefficenti dei vari vettori u, cosa possibile in ogni spazio vettoriale, diventa

Quest'ultima relazione è sicuramente soddisfatta se troviamo degli scalari x₁, x₂, ... , x_m non tutti nulli tali che

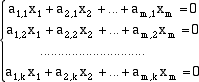
Il sistema che abbiamo scritto è un sistema omogeneo di k equazioni lineari in m incognite e m è più grande di k. Questo sistema ammette sempre una soluzione non nulla. Infatti, se la prima equazione ha tutti i coefficienti nulli, cioé se la prima equazione è 0=0, eliminando quella equazione, ci resta un sistema con una equazione in meno e lo stesso numero m di incognite. Porseguiamo così fino a trovare una equzione non nulla. Ricaviamo da questa una incognita (tra quelle che hanno il proprio coefficiente non nullo) e sostituiamola nelle altre equazioni riducendo così il sistema a un sistema in m-1 incognite e k-1 (o meno) equazioni. Da una soluzione non nulla di questo nuovo sistema, possiamo risalire a una soluzione non nulla per il sistema iniziale. Abbiamo in questo modo ridotto il problema a un sistema più piccolo. Proseguendo in questo modo alla fine arriviamo a un sistema in una sola equazione e almeno due incognite. È ovvio che quest'ultimo sistema ammette sempre una soluzione non nulla.

Questo lemma ci permette di dimostrare il risultato principale relativo alle basi di uno spazio vettoriale.

Teorema VIII 3
Supponiamo che B = {u₁, u₂, ... , u_n} sia una base per uno spazio vettorialeV, allora
       (i) comunque si scelgano n+1 vettori in V, questi sono linearmente dipendenti
      (ii) comunque si scelgano n-1 vettori in V, questi non generano tutto lo spazio.
(dimostrazione)


Ovviamente il teorema implica anche, a fortiori, che se lo spazio vettoriale V ha una base formata da n vettori allora un qualunque insieme di m vettori di V non può essere formato da vettori linearmente indipendenti se m > n, e non può generare tutto lo spazio se m < n. Da questo teorema seguono vari corollari.

Corollario 1
Due basi diverse di uno stesso spazio vettoriale hanno lo stesso numero di elementi.

Infatti, se la prima base ha n elementi, la seconda base non può averne di più perché questi sarebbero indipendenti e nello spazio non ci sono più di n vettori indipendenti. D'altra parte i vettori della seconda base non possono neppure essere meno di n perché in quel caso avremmo meno di n vettori che generano lo spazio.

Definizione
Se uno spazio vettoriale V ammette una base si chiama la dimensione dello spazio e si indica con dim V il numero di vettori della base.

Poiché due basi diverse hanno sempre lo stesso numero di elementi questo numero definisce una caratteristica strutturale dello spazio V che non dipende dalla particolare base scelta.

Negli esempi che abbiamo visto di spazi vettoriali la dimensione si calcola facilmente. Per i vettori geometrici abbiamo che:

• Lo spazio W_r dei vettori di una retta r ha dimensione 1 essendo generato da un vettore non nullo di quella retta
  
  
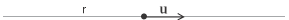
  W_r = Span(u)       dim W_r = 1
  
• Lo spazio W dei vettori di un piano ha dimensione 2 essendo generato da due vettori linearmente indipendenti
  
  
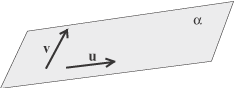
  W = Span(u,v)        dim W = 2
  
• Lo spazio V di tutti i vettori geometrici ha dimensione 3 essendo generato da tre vettori linearmente indipendenti
  
  
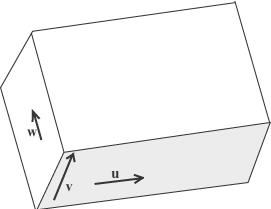
  V = Span(u,v,w)       dim V = 3
  

Lo spazio dei quadrati magici 3x3 ha dimensione 3 perché ha una base formata da tre quadrati magici.

Conoscere una base di uno spazio vettoriale è molto utile perché permette di descrivere tutti gli infiniti vettori dello spazio come combinazioni lineari di un insieme finito di vettori e questo in modo unico. Precisamente

Corollario 2
Se V è uno spazio vettoriale di dimensione n e se B = {u₁, u₂, ... , u_n} è una sua base, allora ogni vettore di V si scrive in modo unico come combinazione lineare dei vettori della base. In altri termini se

allora     a₁ = b₁  ,     a₂ = b₂    , ... ,   a_n = b_n   .
(dimostrazione)

I coefficienti a₁, a₂, ... , a_n che esprimono il vettore v come combinazione lineare dei vettori della base sono dunque univocamente determinati dal vettore v. Poiché questi coefficienti cambiano se, pur restando fisso il vettore, cambia la base, si chiamano le componenti del vettore v nella base B.

Un procedimento spesso efficace per trovare una base di un dato spazio vettoriale si basa, come abbiamo accennato sopra, sul teorema 3. Più precisamente:

• Si cerca un vettore non nullo u₁ dello spazio V. Se tale vettore non esiste vuol dire che V ha solo il vettore nullo
  V = {0} e dim V = 0
  se invece tale vettore esiste {u₁} è linearmente indipendente e si va al punto successivo
• se {u₁} genera tutto lo spazio allora è una base e
  V = Span (u₁) e dim V= 1
  altrimenti esiste un vettore u₂ che non è multiplo di u₁. I vettori u₁ e u₂ sono, per il teorema 3, linearmente indipendenti e si va al punto successivo
• se {u₁, u₂} generano tutto lo spazio allora sono una base e
  V = Span (u₁, u₂) e dim V= 2
  altrimenti esiste un vettore u₃ che non è combinazione lineare di u₁ e u₂. I vettori u₁, u₂, u₃ sono linearmente indipendenti, per il teorema 3, e si va al punto successivo.
• se {u₁, u₂, u₃} generano tutto lo spazio allora sono una base
  V = Span (u₁, u₂,u₂) e dim V= 3
  altrimenti esiste un vettore u₄ che non è combinazione lineare di u₁ e u₂, u₃. I vettori u₁, u₂, u₃ , u₄ sono linearmente indipendenti per il teorema 3, e si prosegue ricorsivamente.

Se si volesse implementare questa strategia in un programma al calcolatore, sarebbe necessario indicare un algoritmo per calcolare esplicitamente, a ogni passo, l'eventuale vettore che non è combinazione degli altri cosa non facile. Nella pratica, volendo usare questo procedimento, ci si orienta a occhio seguendo una qualche intuizione ma in molti casi questa non basta e non si sa come procedere come ad esempio nel caso che abbiamo visto dei quadrati magici. Sviluppando la teoria, riusciremo, per altra via, a dare un esplicito ed effettivo algoritmo per risolvere completamente il problema. In ogni caso, se il procedimento che abbiamo descritto ha termine dopo un numero finito di passi (cosa che non sempre avviene) lo spazio vettoriale V ha dimensione finita altrimenti V ha dimensione infinita.
Vi sono moltissimi esempi di spazi vettoriali di dimensione infinita, questi spazi sono tipicamente degli spazi di funzioni: le funzioni, ad esempio di R in R, possono sommarsi tra loro e moltiplicarsi per uno scalare, esiste la funzione identicamente nulla e la funzione opposta e tutti i requisiti per essere uno spazio vettoriale sono banalmente verificati. Non è difficile fornire una famiglia infinita di funzioni linearmente indipendenti: consideriamo per ogni intero positivo n la funzione

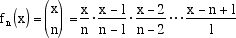
le funzioni binomiali hanno la ovvia proprietà che f_n(i) = 0 per ogni intero positivo i < n e f_n(n) = 1. Questa proprietà ci aiuta a vedere che queste n funzioni sono linearmente indipendenti. Se fosse infatti

la funzione a primo membro dovrebbe, come quella a secondo, annullarsi per ogni valore di x. Ma per x=1 la relazione precedente si riduce a a₁f₁(1) = 0 cioé a₁ = 0. Per x=2 abbiamo, essendo a₁=0, a₂f₂(2) = 0 e quindi anche a₂ = 0. Sostituendo gli altri valori interi fino a x=n troviamo alla fine a_nf_n(n) = 0 e quindi anche a_n = 0. Comunque sia grande l'intero n troviamo dunque n funzioni linearmente indipendenti e quindi lo spazio non può avere una base finita. L'indipendenza lineare di queste funzioni permette di dimostrare il così detto principio di identità.
Questo principio afferma che se due polinomi P(x) e Q(x) a coefficienti reali sono uguali per tutti i valori della variabile allora i due polinomi hanno gli stessi coefficienti e, in particolare, hanno lo stesso grado. Facendo la differenza tra i due polinomi questo principio si riduce al seguente: se F(x) è un polinomio che si annulla per tutti i valori della variabile allora i coefficienti del polinomio F sono tutti nulli. Questa proposizione, nel nostro linguaggio, si riduce a dire che i polinomi 1, x, x², ... , xⁿ sono linearmente indipendenti. La dimostrazione di questo fatto, che generalmente viene fatta usando un passaggio al limite, si può anche ottenere usando i concetti che abbiamo ora introdotto.

Vediamo ora alcune conseguenze di questi teoremi.

Corollario 3
Se V è uno spazio vettoriale di dimensione finita e se {u₁, u₂, ... ,u_k} è un sistema di vettori linearmente indipendenti, allora è sempre possibile completare il sistema fino ad arrivare ad una base di V.
(dimostrazione)

Corollario 4
Se V è uno spazio vettoriale di dimensione n allora
       (i) n vettori linearmente indipendenti generano V
       (ii) n vettori che generano V sono linearmente indipendenti
(dimostrazione)

Corollario 5
Sia V uno spazio vettoriale di dimensione finita e W un suo sottospazio. Allora