Lezioni di Geometria

Franco Ghione


Capitolo IX



IX 1. Somma e intersezione di sottospazi vettoriali

Sia V uno spazio vettoriale e siano U e W due suoi sottospazi vettoriali. L'intersezione di U e W è l'insieme formato da tutti quei vettori di V che appartengono sia ad U che a W. Tale insieme si denota col simbolo . Non è difficile dimostrare che

Proposizione IX 1
Se U e W sono due sottospazi vettoriali di V allora è un sottospazio vettoriale di V.
(dimostrazione)

Il fatto che 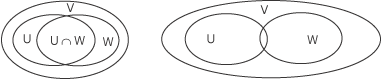sia uno spazio vettoriale è molto importante perché ci pemette di applicare in questo caso la teoria generale degli spazi vettoriali in particolare la teoria della base e della dimensione. Un problema che, ad esempio, si pone è quello di calcolare la dimensione di . E' intuitivamente immaginabile che questa dimensione dipenda anche dalla dimensione dello spazio ambiente V


Nella figura abbiamo rappresentato gli elementi dei tre spazi vettoriali con dei diagrammi di Venn che mostrano la struttura reticolare delle reciproche inclusioni. Nella figura di sinistra, dato che lo "spazio è poco" (V ha dimensione bassa) i due sottospazio U e W non possono distaccarsi troppo e quindi la loro intersezione non può essere troppo piccola, mentre nella figura di destra essendoci molto più spazio l'intersezione può essere piccola.
Per capire bene questa questiuone occorre introdurre anche lo spazio somma: il piú piccolo sottospazio di V che contiene sia U che W. Precisamente se U e W sono due sottospazi vettoriali di V si definisce lo spazio somma, spazio denotato con U + W, il seguente


U + W = {u + w : u U, w W}

Tale insieme si ottiene dunque sommando in tutti i modi possibili un vettore di U con un vettore di W: Ad esempio se sommiamo u + 0 per ogni u di U troviamo un vettore di U + W dato che u appartiene a U e 0 appartiene a W. Ne segue che U U + W. Analogamente si vede che W U + W. Anche in questo caso possiamo facilmente dimostrare che U + W è un sottospazio vettoriale di V:

Proposizione IX 2
Se U e W sono due sottospazi vettoriali di V allora U + W è un sottospazio vettoriale di V.
(dimostrazione)

Se U = Span(u1,u2, ... ,uh) e W = Span(w1,w2, ... ,wk) , allora è evidente che

Span(u1,u2, ... ,uh) + Span(w1,w2, ... ,wk) = Span(u1,u2, ... ,uh, w1,w2, ... ,wk)

Questo fatto fa capire come lo spazio U + W sia il più piccolo sottospazio vettoriale di V che contiene sia U che W dato che ogni tale sottospazio deve necessariamente contenere i vettori u1,u2, ... ,uh, w1,w2, ... ,wk e le loro combinazioni lineari.

IX 2. La formula di Grassmann



           
H. G. Grassmann (1809-1877)                     G. Peano (1858-1932)         

Grassmann è uno dei fondatori della teoria astratta degli spazi vettoriali. La sua opera (l'Ausdehnungslehre che significa teoria dell'estensione) fu poco capita dai contemporanei tanto che alla fine Grassmann spostó i suoi interessi verso altre discipline come la botanica, la linguistica, le lingue orientali. Fu soprattutto il matematico italiano Giuseppe Peano che riprese gli studi di Grassmann e che, nel 1888, pubblicò il suo libro Calcolo geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle operazioni della logica deduttiva dove vengono sviluppate nel caso di spazi di di vettori geometrici il "calcolo geometrico" basato sulle operazioni sui vettori introdotte da Grassmann nel caso più generale di spazi vettoriali astratti.


La formula di Grassmann stabilisce una relazione tra le dimesioni dello spazio somma e dello spazio intersezione ed è di estrema utilità nello studio degli iperspazi.

Formula di Grassmann
Sia V uno spazio vettoriale di dimesione finita e siano U e W due suoi sottospazi vettoriali. In queste ipotesi risulta

dim(U + W) = dim U + dim W - dim

Dimostrazione.
Lo spazio essendo un sottospazio vettoriale di V che ha dimensione finita, ammette una base. Sia z1, z2, ... , zh una sua base:

= Span(z1, z2, ... , zh)

Possiamo, per il corollario 3 prolungare questa base a una base di U e a una base di W dato che U 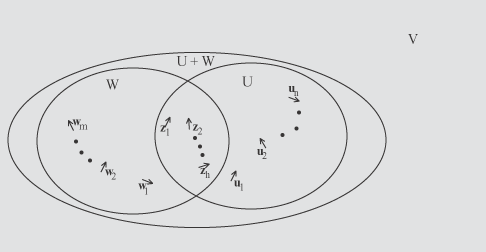e W . Siano dunque queste basi quelle indicate nella formula seguente

U = Span(z1, z2, ... , zh,u1, u2, ... , un )     e    W = Span(z1, z2, ... , zh, w1, w2, ... , wm)


Dico che i vettori z1, z2, ... , zh, u1, u2, ... , un, w1, w2, ... , wm, sono una base di U + W. E' intanto chiaro che questi vettori generano tutto lo spazio U + V. Se infatti u + w è un vettore di U + W allora

u = a1z1 + a2z2 + ... + ahzh + b1u1 + b2u2 + ... + bnun
v = c1z1 + c2z2 + ... + chzh + d1w1 + d2w2 + ... + dmwm

sommando i due vettori e raccogliendo i termini simili otteniamo

u + w = (a1 + c1)z1 + (a2 + c2)z2 + ... + (ah + ch)zh +
+ b1u1 + b2u2 + ... + bnun + d1w1 + d2w2 + ... + dmwm

che risulta una combinazione lineare dei vettori z1, z2, ... , zh, u1, u2, ... , un w1, w2, ... , wm i quali quindi generano U + V.
Resta da dimostrare che quei vettori sono linearmente indipendenti. Consideriamo allora una loro combinazione lineare nulla e dimostriamo che in questo caso tutti i coefficienti della combinazione sono nulli. Sia

a1 z1 + a2z2 + ... + ahzh +
+ b1u1 + b2u2 + ... + bnun + c1w1 + c2w2 + ... + cmwm = 0

una combinazione lineare nulla. Abbiamo che il vettore


w = -(c1w1 + c2w2 + ... + cmwm)

appartiene a W ma anche a U dato che

w = -(c1w1 + c2w2 + ... + cmwm) =a1 z1 + a2z2 + ... + ahzh +
+ b1u1 + b2u2 + ... + bnun

Ne segue che w appartiene a e quindi si può scrivere come combinazione lineare dei vettori della base di . Dunque

w = -(c1w1 + c2w2 + ... + cmwm) = d1z1 + d2z2 + ... + dhzh)

cioé

c1w1 + c2w2 + ... + cmwm+ d1z1 + d2z2 + ... + dhzh = 0

Ora poiché i vettori z1, z2, ... , zh, w1, w2, ... , wm sono linearmente indipendenti essendo una base di W, tutti i coefficienti debbono essere nulli, in particolare: c1 = c2 = ... = cm = 0.
La relazione dalla quale siamo partiti si riduce allora alla relazione

a1 z1 + a2z2 + ... + ahzh + b1u1 + b2u2 + ... + bnun= 0

e quindi essendo i vettori z1, z2, ... , zh,u1, u2, ... , un una base per U, anche questi coefficienti devo essere nulli. Risulta quindi che dim = k, dim U = n + k, dim W = m + k, dim (U + W) = n + m + k e qunidi

dim (U + W) = dim U + dim W - dim

Esercizi