Lezioni di Geometria

Franco Ghione


Capitolo XIII



Coordinate cartesiane

Lo spazio euclideo tridimensionale si indica con E3: E sta per Euclide, 3 è la dimensione. L'insieme V dei suoi vettori è lo spazio vettoriale dei vettori geometrici. V è uno spazio vettoriale di dimensione 3 dotato di un prodotto scalare. Questi due insiemi sono legati da una relazione fondamentale: a due punti qualunque A e B di E3 è possibile associare in modo univoco un vettore di V: il vettore AB e questa corrispondenza verifica la relazione strutturale seguente:


AB+BC=AC
Inoltre dato un qualunque vettore v di V e un punto O di E3 esiste un unico punto A di E3 tale che

v = OA

Queste proprietà valgono anche se ci restringiamo a piani o rette dello spazio. Precisamente una retta r da luogo anche all'insieme dei suoi vettori cioè dei vettori AB definiti da due punti di r. L'insieme di tali vettori è un sottospazio vettoriale di V di dimensione 1 che si chiama la direzione della retta r e che abbiamo indicato con Wr. Anche in questo caso, dato un qualunque vettore v di Wr e un punto O di r esiste un unico punto A di r tale che v = OA.
Analogamente anche un piano a si porta dietro l'insieme dei suoi vettori. Tale insieme si chiama la giacitura di a ed è un sottospazio vettoriale di V di dimensione 2 che abbiamo indicato con Wa.

Possiamo ora dare il concetto di sistema di riferimento cartesiano. Se r è una retta, un sistema di riferimento cartesiano per r è una coppia (O, i) dove O è un punto della retta, detto origine del sistema di riferimento, e i è un versore di Wr cioè una base ortonormale dello spazio dei vettori di r. Fissato un sistema di riferimento cartesiano su una retta r possiamo associare a ogni punto P di r un numero reale x detto ascissa di P nel riferimento (O,i). Il numero x è quel ben determinato numero che esprime il vettore OP di Wr come multiplo di i: OP = x i.


Il numero x si interpreta, essendo i un versore, come la distanza, con segno, di P da O.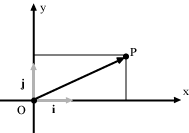
Analogamente se a è un piano e Wa è lo spazio dei suoi vettori, un sistema di riferimento cartesiano per il piano a è una terna (O,i,j) dove O è un punto del piano detto origine1 del sistema di riferimento e {i,j} una base ortonormale per i vettori di a. Fissato un sistema di riferimento cartesiano per il piano a possiamo associare biunivocamente a ogni punto P del piano due numeri reali x e y detti rispettivamente ascissa e ordinata del punto P. I numeri x e y sono quei ben definiti numeri che esprimono il vettore OP come combinazione lineare dei vettori della base: OP = xi + yj.


L'ascissa x rappresenta la distanza di P dall'asse delle ordinate e l'ordinata la distanza dall'asse delle ascisse.

In generale un sistema di riferimento cartesiano nello spazio euclideo è dato quando si sia fissato un punto O di E3 detto origine del sistema di riferimento e una base ortonormale di V che indichiamo, seguendo una notazione usata in fisica, con i, j, k. Una volta che sia stato fissato un sistema di riferimento cartesiano, è possibile associare in modo univoco, ad ogni punto P dello spazio una terna ordinata di numeri reali detti le coordinate cartesiane di P nel dato riferimento. Per determinate tali coordinate si considera il vettore geometrico OP e si scrive come combinazione lineare dei vettori i, j e k che formano una base per lo spazio dei vettori geometrici. I coefficienti di questa combinazione lineare, che sono univocamente determinate da P, sono le coordinate di P :

OP = xi + yj + zk

e si scrive P = (x,y,z).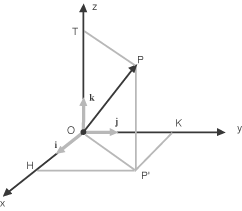
Le tre rette a due a due ortogonali che passano per O e che sono parallele ai vettori i, j e k si chiamano assi coordinati rispettivamente l'asse delle x, l'asse delle y e l'asse delle z.


Se P' è la proiezione ortogonale di P sul piano orizzontale e se H e K sono le proiezioni ortogonali di P' sugli assi x e y rispettivamente, allora

OP = OH + HP' + P'P = xi + yj + zk

e quindi le tre coordinate di P si interpretano come le lunghezze (con segno) dei segmenti

x = OH , y = OK , z = OT

Osserviamo che, essendo i, j, k una base ortonormale di V, le coordinate del punto P si ottengono moltiplicando scalarmente il vettore OP per i tre versori della base:
x = OP.i , y = OP.j , z = OP.k

Se A = (x1,y1,z1) e B = (x2,y2,z2) sono due generici punti dello spazio, la loro distanza è data dal modulo del vettore AB. Poiché AB =AO + OB = OB - OA e poiché, per come sono state definite le coordinate, OA = x1i + y1j + z1k e OB = x2i + y2j + z2k, abbiamo:

AB = (x2 -x1)i + (y2 - y1) j + (z2 - z1)k

(formula 1)


Calcolando il modulo di questo vettore abbiamo la formula che da la distanza tra A e B in funzione delle loro coordinate

(formula 2)


Usando il fatto che la sfera è il luogo dei punti dello spazio che hanno distanza fissa da un dato punto detto centro della sfera, un punto generico P = (x,y,z) dello spazio appartiene alla sfera di raggio r e centro C = (x1,y1,z1) se e solo se
(x-x1)2 + (y-y1)2 + (z-z1)2 = r2

(equazione della sfera)


Ad esempio i punti P dello spazio le cui coordinate verificano l'equazione

x2 + y2 + z2 - 2x = 3

formano una sfera di centro C=(1,0,0) e raggio 2. Infatti completando il quadrato x2-2x troviamo

(x2 - 2x + 1) -1 + y2 + z2 = 3

(x - 1)2 + y2 + z2 = 4

Non è difficile, dati n punti dello spazio dei quali siano note le coordinate, calcolare quelle del loro centro. Abbiamo infatti che, se A1=(a1,b1, c1) , A2=(a2,b2, c2) , ... , An=(an,bn, cn) sono le coordinate degli n punti e se C=(x,y,z) è il centro della configurazione, allora, per definizione di Centro, ponendo R=O,

OA1 + OA2 + ... + OAn = nOC

e quindi, moltiplicando per i

OA1 .i + OA2.i + ... + OAn.i = nOC.i

cioé

a1 + a2 + ... + an = nx

analogamente moltiplicando per j e k. In definitiva abbiamo:



Esercizi