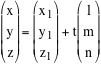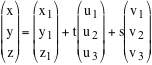|
Lezioni di Geometria Franco Ghione |
 |
Equazioni di una retta
Per trovare le relazioni algebriche che debbono verificare le coordinate dei punti che appartendono ad una retta,
come abbiamo fatto per i piani, dobbiamo trovare una proprietà geometrica, traducibile in termini di vettori, che caratterizzi tutti e soli i punti
di una retta.
Un modo per fare questo consiste nel descrivere i punti della retta come l'insieme delle combinazioni lineari di un vettore non nullo applicati ad uno stesso
punto della retta medesima. Questa strada conduce alle così dette equazioni parametriche della retta. = tu1 i + tu2 j + tu3k Poiché un vettore si scrive in modo unico come combinazione lineare di vettori di una base, da questa relazione
troviamo le equazioni: |
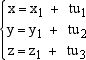 |
|
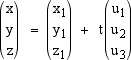 Esempio Cerchiamo le equazioni della retta passante per il punto A = (1,1,0) e B= (0,2,2) come mostrato in figura. 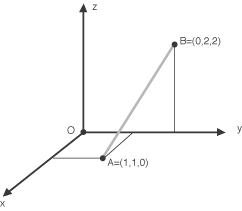
Per scrivere le equazioni parametriche di questa retta dobbiamo trovare un suo punto (e questo può essere il punto A = (1,1,0)
che già conosciamo) e un vettore parallelo alla retta. Visto che conosciamo anche il punto B della retta possiamo scegliere come vettore
parallelo alla retta il vettore AB le cui componenti possono essere calcolate usando la formula 1: Le equazioni si ottengono allora sostituendo i 6 valori noti (le tre coordinate di A e le tre componenti di AB) nelle equazioni precedenti. Troviamo così 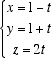
Al variare dei del parametro t troviamo tutti e soli i punti della retta. Ad esempio il punto (3,-1,-4) appartiene alla retta perché si
ottiene in corrispondenza al valore t=-2 del parametro , mentre il punto (1,1,1) non appartiene alla retta perché non è possibile
ottenerlo dalle equazioni precedenti, qualunque sia la scelta di t. Per trovare le caratteristiche geometriche di una retta definita come intersezione di due piani occorre risolvere il sistema precedente
esplicitando le coordinate x, y, z come funzioni di un parametro t. Le tre equazioni così trovare daranno la direzione della retta e un suo punto.
Anziché
trovare delle formule generali a partire dai coefficienti delle equazioni dei due piani indichiamo con un esempio la procedura che abbiamo illustrato. Calcolando y in funzione di x nella seconda equzione troviamo y = 2x-2. Sostituendo questo valore nella prima equzione e calcolando z, troviamo
x-4x+4+z = 2, cioé z = 3x-2.Prendendo x = t troviamo le equazioni: 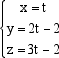 e quindi la retta è parallela al vettore i + 2j + 3k e passa per il punto (0,-2,-2).
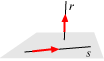
Relazioni di parallelismo e perpendicolarità tra rette e piani.
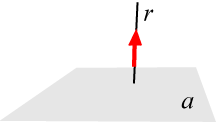
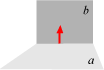
Osserviamo che le ultime due relazioni sono simmetriche. Infatti la retta r è perpendicolare al piano a se e solo se il piano a è perpendicolare alla retta r cosa che si dimostra immediatamente passando all'ortogonale e usando le proprietà di questo operatore.
e quest'ultima relazione si interpreta dicendo che il piano a è perpendicolare alla retta r. Esercizi |