nella quale i numeri a,b,c indicano le coordinate cartesiane del punto C. È anche possibile descrivere i punti di una sfera con equazioni parametriche. Queste equazioni mettono in corrispondenza biunivoca (e bicontinua) i valori di una coppia di parametri con i punti della sfera. Poiché la sfera rappresenta il modello geometrico col quale descrivere la volta celeste e la terra queste "coordinate sferiche" sono state introdotte in tempi antichissimi e tutt'oggi mantengono essenzialmente lo stesso carattere. Per poter rappresentare con una coppia di numeri i punti di una sfera, così come si fa nel piano quando si introducono le coordinate, occore fissare un "sistema di riferimento". Nel caso della sfera occorre fissare un cerchio massimo ¹ che diremo equatore, un polo e una linea meridiana cioé un cerchio massimo che passa per il polo. Questi due cerchi sono l'analogo degli assi cartesiani e il punto A in cui si incontrano l'analogo dell'origine del riferimento.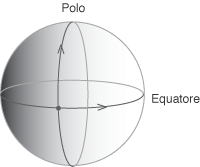

Se P è un qualunque punto della sfera, consideriamo il cerchio massimo che passa per P e per il polo e consideriamo il punto S nel quale tale cerchio interseca l'equatore. L'angolo a definito dall'arco AS è uno dei due parametri e si chiama (con linguaggio geografico) longitudine del punto P, mentre l'angolo b definito dall'arco SP si chiama latitudine del punto P della sfera.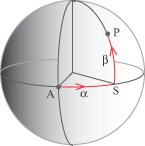

L'angolo a si prende compreso tra -p e p mentre l'angolo b tra -p/2 e p/2. Nel linguaggio classico, gli angoli venivano misurati in gradi, un grado è la 360 parte di un angolo giro e, mancando la considerazione dei numeri negativi, per denotare angoli positivi o negativi venivano usate le parole: "a gradi di longitudine est" vuol dire longitudine +a mentre "a gradi di longitudine ovest" vuol dire longitudine -a. In questo modo l'angolo a è sempre compreso tra 0 e 180 gradi. Analogamente per le latitudini: il termine "nord" vuol dire "+" mentre il termine "sud" vuol dire "-". L'uso dei numeri negativi, ovviamente, non aggiunge nulla al contenuto descrittivo del modello, ma semplifica di molto i calcoli che altrimenti debbono ogni volta contemplare i vari casi possibili.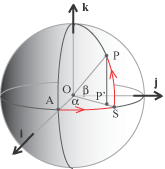
Per scrivere delle equazioni dobbiamo fissare un riferimento cartesiano. Scegliamo il punto O nel centro della sfera e i vettori i, j e k come in figura. Le coordinate del punto P si ottengono proiettando ortogonalmente P sul piano dell'equatore. Sia P' tale proiezione.

Abbiamo OP = OP' + P'P e P'P = r sin(b)k, mentre, guardando sul piano equatoriale, troviamo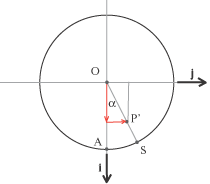

OP' = |OP'|cos(a) i + |OP'|sin(a) j)

e tenendo conto che |OP'| = r cos(b) abbiamo

e quindi, uguagliando le componenti, otteniamo le equazioni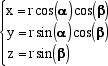

che esprimono le coordinate cartesiane di un punto della sfera di longitudine a e latitudine b. Queste equazioni definiscono, come abbiamo detto, una corrispondenza biunivoca tra i punti di un rettangolo e i punti della sfera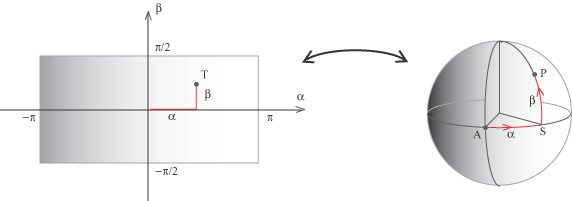

a ogni punto P della sfera corrisponde il punto T=(a,b) del rettangolo e viceversa a ogni punto del rettangolo corrisponde il punto della sfera con latitudone a e longitudine b. La figura seguente riporta nel rettangolo i corrispondenti punti della terra. Questa immagine da un'idea di come agisce la trasformazione.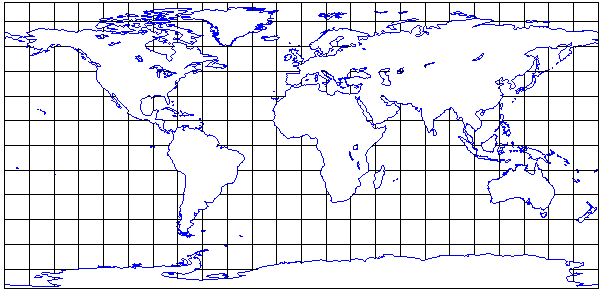

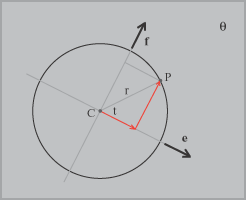
Le considerazioni precedenti ci indicano la strada da seguire per scrivere le equazioni parametriche di una circonferenza della quale sia noto il centro, il raggio e il piano nel quale si trova. Sia C il centro, q il piano e r il suo raggio. Scegliamo una base ortonormale e ed f del piano q e descriviamo i punti P della circonverenza al variare dell'angolo t (0 < t < 2p) che il vettore CP forma con il vettore e

Abbiamo CP = r cos(t) e + r sin(t) f e quindi se O è l'origine delle coordinate il vettore

fornisce le coordinate del punto P al variare del parametro t. Notiamo che in questa formula ogni parte è espressa in termini dei dati del problema: OC è noto perché sono note le coordinate di C =(x₁,y₁,z₁) , e = e₁i + e₂j + e₃k e f = f₁i + f₂j + f₃k sono noti perché è dato il piano q e quindi è possibile calcolare una base ortonormale dello spazio dei suoi vettori, r è dato e t è il paramtro al variare del quale si ottengono tutti i punti della circonferenza. Le equazioni che si ottengono sono le equazioni parametriche della circonferenza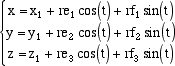

Volendo trovare delle equazioni cartesiane della circonferenza, dobbiamo trovare due superfici che si intersecano lungo la data circonferenza. Vi sono ovviamente moltissime possibilità: una di queste, particolarmente semplice consiste nel prendere la sfera di centro C e raggio r e il piano q. Se ax + by + cz = d è l'equazione cartesiana del piano allora le soluzioni (x,y,z) del sistema in due equazioni e tre incognite

danno le coordinate dei punti che si trovano sia sulla sfera che sul piano e quindi i punti che si trovano nella loro intersezione che è appunto la data circonferenza.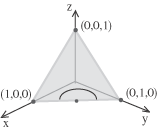
Cerchiamo, ad esempio le equazioni parametriche della circonferenza che si trova sul piano x+y+z=1 e ha centro (1/2,1/2,0) e raggio 1/4.

La spazio dei vettori del piano dato è lo spazio W = Span(i+j+k)^{^} e, come base ortonormale possiamo prendere i vettori

Le equazioni parametriche della circonferenza sono dunque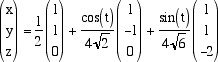

cioé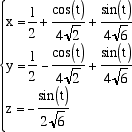

Le equazioni cartesiane della circonferenza sono invece

Un altro modo per rappresentare le coordinate di un punto di una circonferenza in funzione di un parametro si ottiene tramite la così detta proiezione stereografica. Consideriamo ancora una base ortonormale e ed f dello spazio dei vettori del piano della circonferenza e sia C il suo centro. Proiettiamo i punti della circonferenza sulla retta passante per C con la direzione di e a partire dal punto S. Stabiliamo in questo modo una corrispondenza biunivoca tra i punti T della retta e i punti P della circonferenza (tranne il punto S a cui corrisponderebbe un "punto all'infinito"). Per scrivere le equazioni di questa proiezione scegliamo un sistema di riferimento cartesiano sul piano della circonferenza: sia (C,e,f) tale sistema di riferimento (il centro C della circonferenza è l'origine e i vettori e ed f sono una base ortonormale per i vettori del piano). Scegliamo anche come unità di misura il raggio della circonferenza data e chiamiamo u e v gli assi coordinati.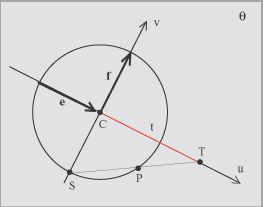

In questo sistema di riferimento, abbiamo come coordinate i valori seguenti: C= (0,0), S=(0,-1) e T=(t,0). La retta ST ha equazione

mentre la circonferenza

L'intersezione della retta con la circonferenza produce il punto S (che non interessa perché è un punto fisso) e il punto P le cui coordinate dipendono biunivocamente da t. Risolviamo il sistema, ricavando la v dall'equazione della retta e sostituendola nell'equazione della circonferenza. Troviamo così una equzione di secondo grado nella sola incognita u che ha la soluzione u=0 (che corriusponde al punto S che non interessa) e la soluzione u=2t/(1+t²) che è l'ascissa del punto P. Usando l'equazione della retta possiamo trovare l'ordinata di quel punto v = (u/t)-1. In definitiva abbiamo le equazioni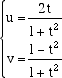

Ricordando la definizione di coordinate cartesiane osserviamo che il vettore CP = u e + vf e quindi se questi vettori sono dati in termini della base i,j,k abbiamo, nel sistema di riferimento (O,i,j,k), le equazioni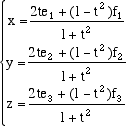

Le formule che abbiamo ottenute associano ad ogni valore del parametro t un punto della circonferenza: esse sono sempre definite perché 1+t² non è mai nullo. La differenza con le equazioni precedenti, che esprimevano le coordinate di un punto della circonferenza usando le funzione seno e coseno (funzioni trascendenti), è che ora le funzioni in gico sono funzioni razionali e possiamo calcolare, per ogni valore di t le coordinate di un punto della circonferenza operando, con le sole le operazioni di somma, prodotto, sottrazione e divisione, su un numero finito di dati. Se ad esempio t è un numero intero o razionale il punto della circonferenza che troviamo ha coordinate razionali: per t=2, ad esempio troviamo il punto (4/5,-3/5) per t=1/2 il punto (4/5,3/5). Questa rappresentazione dei punti di una circonferenza ha grande importanza anche i teoria dei numeri: il problema ad esempio, di trovare due numeri interi a e b tali che la somma dei loro quadrati sia il quadrato di un numero intero, cioé il problema di trovare le soluzioni intere dell'equazione diofantea a² + b² = c² si risolve facilemente prendendo

e dando a t valori interi. Le terne che si trovano sono dette terne pitagoriche perché corrispondono ad atrettanti triangoli rettangoli coi lati interi. Sono ad esempio terne pitagoriche le terne (4,3,5), (6,8,10), (8,15,17) ecc.

Anche la sfera può essere parametrizzata con funzioni razionali cercando di generalizzare nella dimensione tre la proiezione stereografica. Fissiamo un punto S della sfera (polo Sud) e il piano equatoriale. Se P è un qualunque punto della sfera (diverso da S) possiamo considerare la retta SP e intersecare questa retta col piano equatoriale. Troviamo un punto T che è la proiezione di P da S su quel piano.

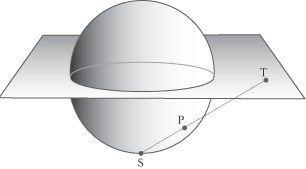
Questa corrispondenza è biunivoca e fa corrispondere a un punto T del piano (punto che dipende da due parametri liberi) un ben determinato punto della sfera dato che una retta incontra la sfera in due punti: uno è S che è fisso e l'altro è P che dipende da T. Per determinare le relazioni analitiche che descrivono questa proiezione dobbiamo fissare un sistema di riferimanto cartesiano. Prendiamo l'origine O del sistema nel centro della sfera, il piano equatoriale come piano x,y e l'unità di misura uguale al raggio della sfera. In questo sistema di riferimento il punto S ha le coordinate S=(0,0,-1), il piano equatoriale ha equazione z=0 , un suo punto T ha le coordinate T=(a,b,0)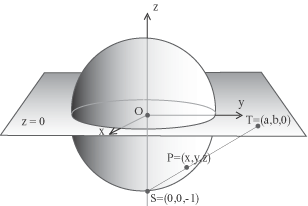

e la sfera ha equazione cartesiana

Per trovare le coordinate del punto P in funzione di a e b scriviamo le equazioni parametriche della retta ST e intersechiamo questa retta con la sfera. Se t è il parametro che descrive i punti della tetta ST, abbiamo le equazioni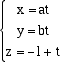

sostituendo questi valori nell'equazione della sfera, troviamo il valore del parametro t corrispondente a un punto della retta che appartiene anche alla sfera. Abbiamo

La soluzione t=0 corrisponde al punto S che non ci interessa, mentre la soluzione t=2/(1+a²+b²) corrisponde al punto P che cerchiamo. Le coordinate di P sono dunque le coordinate del punto della retta ST che corrispondono a questo valore del parametro. Con facili conti troviamo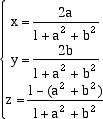

Queste equazioni danno, per ogni scelta dei parametri a e b, un punto della sfera mediante funzioni razionali. Ad esempio per a=1 e b=2 troviamo il punto P=(1/3,2/3,-2/3) che è un punto della sfera dato che la somma dei quadrati di questi tre numeri fa 1.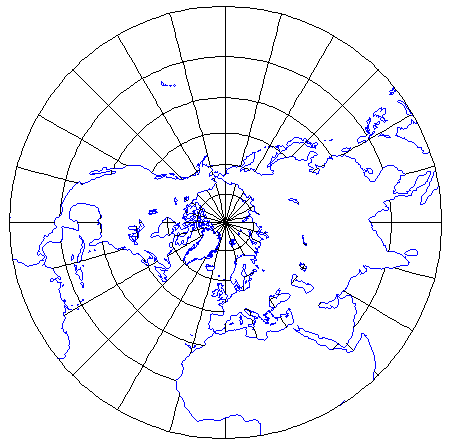
Se ci si limita a rappresentare con la proiezione stereografica l'emisfero nord, abbiamo una mappa tra i punti di questo emisfero e i punti interni al disco del piano (a,b) di centro O e raggio 1: quelli per cui a² + b² < 1 . La figura seguente da un'idea di come agisca sui punti della terra questa rappresentazione

Queste immagini che esemplificano diversi modi di rappresentare i punti della terra mediante equazioni parametriche sono state prese dal sito www.geometrie.tuwien.ac.at/karto/ dove si trovano diverse altre rappresentazioni parametriche usate in geografia.
La proiezione stereografica della sfera su un piano ha una proprietà geometrica di grande importanza: essa trasforma una circonferenza sulla sfera in una circonferenza sul piano. Questa proprietà, già nota ad Apollonio nel III sec. a.C., veniva usata per fare modelli matematici del cielo e dei moti dei corpi celesti. Il cielo viene rappresentato e come una semisfera che ha il suo centro nel punto dove si trova l'osservatore. I corpi celesti, stelle e pianeti, vengono rappresentati con un punto su questa semisfera ottenuto considerando l'intersezione del raggio visivo col quale si osserva il corpo con la volta celeste. La proiezione stereografica della volta celeste su un piano (generalmente un disco) permette di rappresentare le costellazioni, il moto apparente del sole e delle stelle fisse, su un oggetto piatto dando luogo a uno strumento di grande utilità per la navigazione, l'astrolabio, col quale era possibile calcolare, tra l'altro, l'ora e l'orientamento.

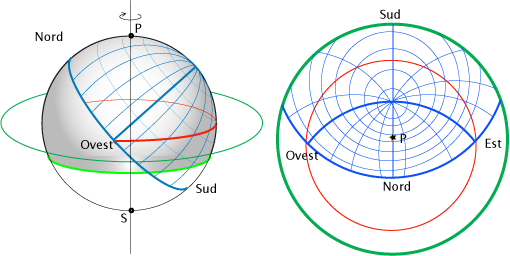
La figura precedente rappresenta la proiezione stereografica dal polo sud sul piano equatoriale, della semisfera visibile da un punto della terra a una latitudine di circa 42 gradi.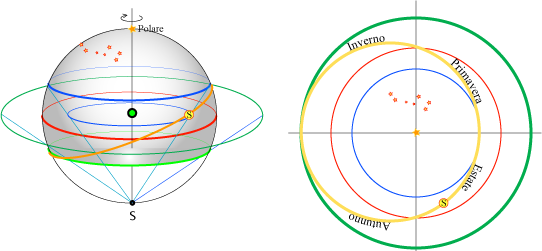

Questa figura rappresenta, con la stessa proiezione stereografica precedente, l'immagine, sul disco dell'astrolabio, del cerchio dell'eclittica dove avviene il moto apparente del sole nel corso dell'anno e delle stelle dell'orsa maggiore. Nel centro dell'astrolabio è posizionata la stella polare per cui ruotando questo disco si simula la rotazione apparente delle stelle e del sole nel cielo. Sovrapponendo i due dischi si può trovare la posizione del corpo celeste sulla semisfera che rappresenta la volta celeste visibile alla data latitudine.
Una completa descrizione interattiva dell'astrolabio si può trovare sul sito del Museo di Storia della scienza di Firenze http://brunelleschi.imss.fi.it/esplora/astrolabio/indice.html

Esercizi difficili