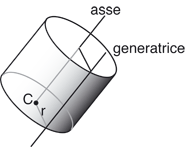Una possibile caratterizzazione geometrica dei punti del cilindro, facilmente traducibile in termini vettoriali, si ottiene osservando che un punto P dello spazio si trova sul cilindro che ha come asse la retta a e raggio r se e solo se la sua distanza da a è r. Ricordiamo infatti che la distanza di un punto P da una retta a è la lunghezza del segmento PH passante per P e perpendicolare alla retta a in H.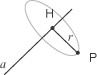

Non è difficile tradurre questa condizione in termini vettoriali. Supponiamo che l'asse del cilindro sia la retta passante per C=(x₁,y₁,z₁) e di direzione u = ai + bj + ck e supponiamo che il vettore u abbia modulo 1.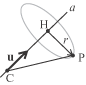

Supponiamo che P=(x,y,z) sia un generico punto dello spazio. Abbiamo HP = CP - CH dove CH è la proiezione ortogonale di CP sulla retta a. Ora P appartiene al cilindro di asse a e raggio r se e solo se |HP| = r. Possiamo calcolare |HP| usando il teorema di Pitagora. Osserviamo infatti che | CH|, dato che il vettore u è di modulo 1, coincide col prodotto scalare |CP.u|= |u||CP||cos(t)| = |CH|. Dunque

La relazione che abbiamo ottenuto caratterizza i punti P=(x,y,z) che apparetengono al cilindro: essa contiene solo le coordinate di C=(x₁,y₁,z₁), che sono assegnate e le componenti del vettore u pure assegnate. Osservando che CP = (x-x₁)i + (y-y₁)j + (z-z₁)k, non è difficile scrivere nella forma di equazione in x,y,z la condizione precedende pervenendo cosí alla equazione cartesiana di un generico cilindro circolare retto:

Non è utile imparare a memoria questa espressione quanto piuttosto imparare il procedimento che abbiamo usato e che ora illustriamo su un esempio.

Esempio
Scrivere l'equazione del cilindro che ha come asse la retta passante per C=(0,1,0) con la direzione j + k e raggio 2.
Sia P=(x,y,z) un punto generico dello spazio, abbiamo CP = xi + (y-1)j + zk e u = (j + k)/|j + k| quindi (CP.u)² = (y+z-1)²/2. Il punto P è dunque un punto del nostro cilindro se e solo se

svolgendo i calcoli e ordinando i termini dell'equazione troviamo

che rappresenta l'equazione cartesiana del cilindro cercato.

Come 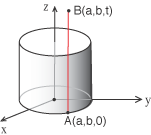si vede questa equazione ha una forma difficilmente riconoscibile. Saranno necessari strumenti più raffinati per poter riconoscere la forma della superficie a partire dalla sua equazione cartesiana.
Notiamo tuttavia che, se il sistema di riferimento viene scelto in modo più attinente alla geometria del cilindro, la situazione si semplifica di molto. Possiamo prendere come origine del sistema di riferimento il punto C che è il centro della circonferenza di base e come asse, la retta per C con la direzione di uno degli assi coordinati. Nel caso ad esempio che sia C=(0,0,0) e u = k, l'equazione del cilindro diventa

cioé

x² + y² = r²

equazione nella quale non compare la variabile z. Il significato geometrico di questa circostanza si spiega facilmente: infatti se un punto A=(a,b,0) appartiene alla superficie, cioè le sue tre coordinate soddisfano l'equazione x² + y² = r², allora per qualunque valore di t, i punti di coordinate (a,b,t) verificano l'equazione e quindi appartengono alla superficie. Ma questi punti sono i punti della retta parallela all'asse delle zeta passante per il punto A. Ne segue allora che la superficie contiene tutti i punti di questa retta.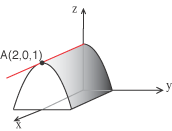
E' questo un fenomeno nuovo rispetto alla geometria analitica piana che dipende dal fatto che lo spazio ha dimensione tre e che una superficie, rappresentata da una equazione cartesiana, ha dimensione 2 e questa superficie, come nel caso del cilindro circolare, può contenere infinite rette. Ogni volta quindi che nell'equazione cartesiana di una superficie non compare una variabile ciò significa che quella superficie, se contiene un punto A, contiene di conseguenza tutta la retta passante per A e parallela all'asse della variabile mancante. Ad esempio la superficie

y² + z = 1

è definita da una equazione che non contiene la variabile x. Poiché il punto A=(2,0,1) appartiene alla superficie dato che ne verifica l'equazione, ogni punto (t,0,1) al variare di t verifica l'equazione perché nell'equazione non compare la variabile x. Ma i punti con queste coordinate sono i punti della retta (disegnata in rosso) passante per A e parallela all'asse delle x. Si riconosce in questo modo che la forma della superficie è quella di un cilindro che ha come base la parabola del piano y,z di equazione z = 1 - y² e asse parallelo all'asse delle x.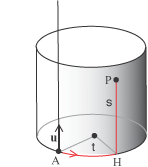

Anche i cilindri circolari possono descriversi con delle equazioni parametriche. Un modo per fare questo è quello di fissare un punto A sulla base del cilindro e un versore u parallelo alla generatrice. Il punto A gioca il ruolo di "origine" mentre la circonferenza di base e la generatrice per A giocano il ruolo di "assi coordinari". I due parametri coi quali determiniamo la posizione di un qualunque punto P del cilindro, parametri, detti in questo caso coordinate cilindriche, sono l'angolo t e la distanza s = PH come in figura

Non è difficile scrivere l'espressione analitica con la quale si ottengono le coordinate cartesiane di un punto P del cilindro in funzione dei due parametri t ed s. Se x=f(t), y=g(t) e z=h(t) sono le equazioni parametriche della circonferenza di base e se u = u₁i + u₂j + u₃k, allora le equazioni parametriche del cilindro sono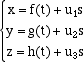

Se facciamo variare l'angolo t tra 0 e 2 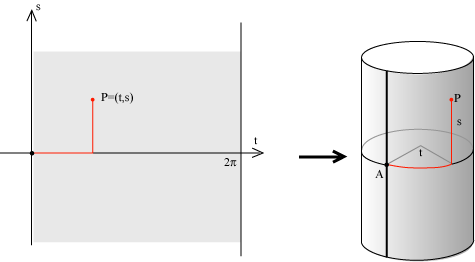e il parametro s in R le equazioni precedenti definiscono una applicazione dallo spazio dei parametri (t,s) nella superficie del cilindro: ad ogni punto della striscia compresa tra 0 e 2 corrisponde un ben definito punto del cilindro. I due bordi della striscia si applicano sulla stessa direttrice del cilindro quella che passa per il punto A che corrisponde ai valori t=0 e s=0.

le rette verticali della striscia si trasformano nelle generatrici del cilindro e la trasformazione pu� essere pensata come una striscia di piano che si avvolge intorno a una circonferenza.

Come esempio, scriviamo ora le equazioni parametriche del cilindro che ha come asse la retta passante per C=(0,1,0) con la direzione j + k e raggio 2. Dobbiamo prima di tutto scrivere le equazioni parametriche della circonferenza che ha centro nel punto C, raggio 2 e che si trova sul piano y+z=1 (il piano passante per C e perpendicolare all'asse). Una base per i vettori di quel piano è data dai vettori i e j-k. Ortonormalizzando la base e scrivendo le equazioni della circonferenza in quella base troviamo

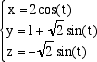e quindi le equazioni del cilindro sono invece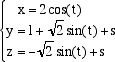

Le equazioni parametriche del cilindro di equazione cartesia x² + y² = r² sono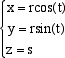

XVII 2. Coni

Nello stesso modo col quale abbiamo studiato i cilindri possiamo studiare i coni circolari retti. Un cono circolare retto si ottiene ruotando una retta detta generatrice intorno a una retta fissa detta asse che interseca la generatrice in un punto V detto il vertice del cono. Un generico punto P della generatrice descrive quindi una circonferenza che ha il centro sull'asse, il raggio uguale alla distanza di P dall'asse e si trova sul piano per P perpendicolare all'asse.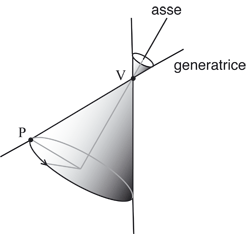

La caratterizzazione geometrica dei punti del cono è moto semplice. Sia 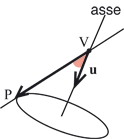l'angolo acuto formato dalle due rette e sia u un versore con la direzione dell'asse. Un generico punto P dello spazio si trova sul cono se e solo se l'angolo tra il vettore u e il vettore VP resta costante (questo angolo è in una falda del cono e - nell'altra falda)

Poiché il coseno dell'angolo tra due vettori si esprime in termini del loro prodotto scalare, la condizione si realizza, essendo u un versore, se e solo se

|u . VP| _/ |VP| = cos()

essendo cos() il coseno dell'angolo acuto tra l'asse e la generatrice.
Come nel caso dei cilindri, l'equazione vettoriale precedente si può facilmente tradurre in una equazione cartesiana: il vertice V=(x₁,y₁,z₁) e il versore u = ai + bj + ck sono dei dati del problema e, se P=(x,y,z) è un punto generico dello spazio, risulta VP = (x-x₁)i + (y-y₁)j + (z-z₁)k. L'equazione diventa dunque

[a(x-x₁) + b(y-y₁) + c(z-z₁)]² = cos²() [(x-x₁)² + (y-y₁)² + (z-z₁)²]

Anche in questo caso non conviene scrivere esplicitamente questa equazione sciogliendo le parentesi dato che il risultato saerebbe poco significativo e di difficile memorizzazione.
Naturalmente, se scegliamo il sistema di riferimento cartesiano tenendo conto della geometria del cono l'equazione che ne deriva è molto semplice. Mettiamo l'origine degli assi nel vertice del cono e scegliamo uno degli assi coordinati come asse del cono, ad esempio l'asse delle z. In questa situazione V=(0,0,0), u = k e VP = xi + yj + zk. Eseguendo il prodotto scalare otteniamo u.VP = z e |VP|² = x² + y² + z² e quindi l'equazione del cono risulta essere

c²x² + c²y² +(c²-1)z² = 0

dove c è il coseno dell'angolo acuto formato dalla generatrice e dall'asse. Introducendo questo angolo l'equazione precedente si può anche scrivere come

x² + y² = tan²() z²

Questa equazione mette bene in evidenza il fatto che, se intersechiamo la superficie con un piano z = z₁ perpendicolare all'asse troviamo una circonferenza di raggio r = z₁tan()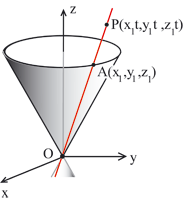

Notiamo la forma dell'equazione che abbiamo trovato: si tratta una equazione omogenea di secondo grado che contiene solo i quadrati delle variabili. In generale possiamo vedere che ogni equazione della forma

ax² + by² + cz² = 0

rappresenta una superficie conica col verice nell'origine. Ciò significa che se un punto A=(x₁,y₁,z₁) appartiene alla superficie, cioé se le sue coordinate verificano l'equazione, ogni altro punto che si trovi sulla retta OA verifica ancora la stessa l'equazione. Infatti un punto P della retta OA ha le coordiante P =( x₁t ,y₁t ,z₁t) e queste verificano l'equazione dato che

a(x₁t)² + b(y₁t)² + c(z₁t)² = t²[ax₁² + by₁² + cz₁²] = t².0 = 0

per ogni valore di t.

In generale un polinomio di secondo grado in tre variabili F(x,y,z) si dice omogeneo se, risulta identicamente (cioé per ogni scelta di x,y,z,t)

F(tx,ty,tz) = t²F(x,y,z)

Questa condizione algebrica, che si riduce al fatto che l'equazione è una somma di monomi di grado due, si riflette geometricamente nel fatto che, la superficie che ha equazione F(x,y,z)=0 è un cono col vertice nell'origine del sistema di riferimento. Ciò vuol dire che se la superficie contiene un punto A diverso da O contiene tutti i punti della retta OA. Tali coni si chiamano coni quadratici dato che la loro equazione è di secondo grado.
Ad esempio l'equazione

x² - yz - z² = 0

rappresenta un cono "parabolico" dato che intersecando la superficie col piano z = 1 troviamo la parabola y = x² - 1 e quindi la superficie è formata da dai punti delle rette che congiungono O al punto P=(x₁,y₁,1) con y₁ = x₁² - 1. Nella figura abbiamo rappresentato in rosso la retta che congiunge il punto A=(2,3,1) con O.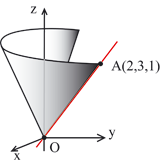

Le equazioni parametriche di un cono circolare retto si scrivono nelle stesso modo col quale si scrivono quelle relative a un cilindro circolare retto. Se x=f(t), y=g(t), z=h(t) sono le equazioni parametriche di una circonferenza perpendiacolare all'asse e se V=(x₁,y₁,z₁) sono le coordinate del vertice del cono, le equazioni parametriche si scrivono scrivendo le equazioni parametriche della retta che congiunge V col punto generico (f(t),g(t),h(t)) della circonferenza

Esercizi