Unità 7

Lezioni di Geometria

Franco Ghione

Le fibre di una applicazione lineare.

Una applicazione lineare, un morfismo di uno spazio vettoriale V in uno spazio vettoriale W è innanzi tutto una applicazione L dell'insieme V nell'insieme W

che, come abbiamo visto, conserva la struttura vettoriale. In questo capitolo vogliamo studiare la "forma" della applicazione lineare, la sua struttura. Vogliamo capire in cosa si differenziano, come si descrivono, con quali immagini possiamo averne una idea intuitiva.
La cosa principale di un morfismo è capire la partizione delle sue fibre. Dato un vettore w del codominio W la fibra su tale vettore è l'insieme dei vettori v del dominio che hanno come immagine w. Si tratta in altre parole dell'immagine inversa del vettore w. Il simbolo con cui si indica la fibra su w è L^-1(w) e dunque la sua definizione formale è

Le fibre, sono dei sottoinsiemi di V che possono essere vuoti (se w non appartiene all'immagine di L) ma che, in generale ricoprono tutto V e non hanno punti in comune (dimostrazione). Esistono essenzialmente 4 tipi di morfismi che possiamo rappresentare schematicamente con le 4 immagini seguenti. In tutte, dominio è uno spazio V grigio, il codominio uno spazio W rosa, e la legge che fa passare dal dominio al codominio è la proiezione verso il basso lungo la verticale.

Nella prima figura l'applicazione è iniettiva l'immagine di L è uguale al codominio W e L è una corrispondenza iniettiva e suriettiva, le fibre sono formate da un singolo punto; l'applicazione è biunivoca o, come anche si dice, uno a uno: a un punto di V corrisponde un punto di W e, viceversa, un punto di W proviene da un unico punto di V. Nella figura accanto l'applicazione è ancora iniettiva, l'immagine di L, che si denota con Im L, è però un sottoinsieme proprio di W (è precisamente un sottospazio vettoriale del codominio) e la fibra su w è vuota, se w non appartiene all'immagione di L, un punto in caso contrario.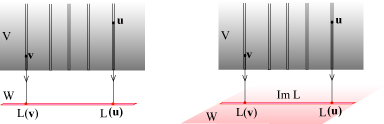

In queste figure invece le fibre sono infinite e sono formate dagli infiniti vettori che si trovano sui "binari" verticali di V. Nella prima figura il morfismo ha delle fibre infinite ed è suriettivo, mentre nel secondo caso il morfismo ha sempre delle fibre infinite ma non è suriettivo.
La teoria che ora svilupperemo permetterà di capire rigorosamente la struttura di una applicazione lineare e darà gli strumenti necessari per calcolare esplicitamente e per via algoritmica le fibre di un dato morfismo. La questione è della massima importanza dato che generalmente le soluzioni di una equazione o di un sistema di equazioni, qualunque sia la loro natura e il numero di incognite, si pone sempre nei termini di fibre. Se infatti x denota il vettore delle incognite, il problema si può porre sempre nella forma

L(x)= b

e dunque le soluzioni sono gli elementi della fibra di L su b.

Di tutte le fibre, la più importante è il nucleo dell'aplicazione lineare L denotato col simbolo Ker L e definito nel modo seguente:

L'importanza di questo sottoinsieme di V consiste nel fatto, cruciale, che esso, a differenza di tutte le altre fibre, è un sottospazio di V: se prendiamo cioè due qualunque elementi v₁ e v₂ di Ker L e li combiniamo linearmente tra loro, troviamo ancora elementi di Ker L. Infatti comunque si prendano gli scalari a₁ e a₂ il vettore a₁v₁ + a₂v₂ è ancora un elemento del nucleo dato che, essendo L lineare,

L(a₁v₁ + a₂v₂) = a₁L(v₁) + a₂L(v₂) = 0

dal momento che L(v₁) = 0 e L(v₂) = 0. Questo fatto ci permette di applicare allo spazio vettoriale Ker L tutti i concetti che abbiamo introdotto in generale per gli spazi vettoriali. In particolare Ker L ha una dimensione e può essere descritto con una base. La sua dimensione è legata alla dimesione dell'immagine dell'applicazione lineare L da un fondamentale teorema del quale ora diamo l'enunciato e la dimostrazione. Questo teorema ci permetterà di capire esattamente la forma del morfismo e quale dei 4 casi raffigurati precedentemente sia quello in esame.

Teorema (di struttura sulle applicazioni lineari)
Sia L una applicazione lineare dello spazio vettoriale V nello spazio vettoriale W e supponiamo che V sia di dimensione finita. Allora

dim V = dim Ker L + dim Im L

Dimostrazione
Dato che Ker L è uno spazio vettoriale ammette una base.
Sia {u₁, u₂, ... , u_q} una base di Ker L.
Anche Im L è uno spazio vettoriale (un sottospazio di W) e possiamo trovarne una base.
Sia {w₁, w₂, ... , w _r} una base di Im L.
Il teorema sarà dimostrato se dimostriamo che dim V = q + r.
Per fare questo cerchiamo una base di V formata da q + r vettori, cerchiamo cioè q + r vettori di V linearmente indipendenti e che generino tutto lo spazio. Di questi q li abbiamo già: sono i vettori della base di Ker L che essendo un sottospazio di V sono vettori di V linearmente indipendenti. Per completare la base non possiamo aggiungere a questi i vettori w₁, w₂, ... , w_r dal momento che questi non sono vettori di V ma vettori del codominio W. Dato però che questi vettori si trovano nell'immagine di L, per ogni vettore w_j possiamo prendere un vettore v_j nella fibra L^-1(w_j) cioè tale che

L(v_j) = w_j

Abbiamo in questo modo costruito q + r vettori di V : {u₁, u₂, ... , u_q, v₁, v₂, ... , v_r}.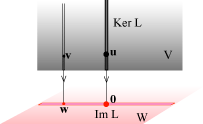

Dimostriamo ora che questi vettori sono una base di V.
I vettori {u₁, u₂, ... , u_q, v₁, v₂, ... , v_r} sono linearmente indipendenti. Per vedere questo dobbiamo verificare che l'unica loro combinazione lineare nulla è quella banale. Sia

a₁u₁ + a₂u₂ + ... + a_qu_q + b₁v₁ + b₂v₂ + ... + b_rv_r = 0

applicando l'applicazione L otteniamo, dato che L è lineare e che L(u_i) = 0 (i=1,2,...,q)

b₁L(v₁) + b₂L(v₂) + ... + b_rL(v_r) = b₁w₁ + b₂w₂ + ... + b_rw_r = L(0) = 0

ma, dato che i vettori w_j (j=1,2,...,r) sono vettori di W linearmente indipendenti, ciò può avvenire se e solo se b₁ = b₂ = ... = b_r = 0. Tornando alla realzione iniziale, se le b sono nulle, resta

a₁u₁ + a₂u₂ + ... + a_qu_q = 0

e, dato che anche i vettori u_i (i=1,2,...,q) sono vettori (di V) linearmente indipendenti, ciò significa che anche le a sono tutte nulle. In definitiva la sola possibile combinazione lineare del vettori u e v è quella banale, quindi tali vettori sono linearmente indipendenti.
I vettori {u₁, u₂, ... , u_q, v₁, v₂, ... , v_r} generano tutto V. Per vedere questo dobbiamo verificare che ogni vettore di V si può scrivere come combinazione lineare di questi q + r vettori. Sia v un qualunque vettore di V. Poichè L(v) è nell'immagine di L può scriversi come combinazione lineare dei vettori w_j (j=1,2,...,r) che sono una sua base. Abbiamo dunque, essendo L lineare,

L(v)= b₁w₁ + b₂w₂ + ... + b_rw_r = b₁L(v₁) + b₂L(v₂) + ... + b_rL(v_r) =
= L(b₁v₁ + b₂v₂ + ... + b_rv_r)

facendo la differenza troviamo

L(v - (b₁v₁ + b₂v₂ + ... + b_rv_r)) = 0

perciò il vettore v - (b₁v₁ + b₂v₂ + ... + b_rv_r) si trova nel nucleo di L e come tale si scrive come combinazione lineare dei suoi generatori

v - (b₁v₁ + b₂v₂ + ... + b_rv_r) = a₁u₁ + a₂u₂ + ... + a_qu_q

e , in definitiva,

v = a₁u₁ + a₂u₂ + ... + a_qu_q + b₁v₁ + b₂v₂ + ... + b_rv_r

come volevamo dimostrare.

Esempio
Consideriamo la proiezione L di R³ in R² definita da

L((x₁,x₂,x₃)) = (x₁,x₂)

Questa applicazione è chiaramente lineare e Im L = R². Il suo nucleo ha quindi dimensione 1 dato che dim Ker L = dim V - dim Im L = 3-2 = 1. Possiamo rappresentare questa proiezione con una immagine mentale del tutto fedele a questa situazione. Identifichiamo la terna (x₁,x₂,x₃) con un punto dello spazio cartesiano (lo spazio cioé nel quale sia stato fissato un sistema di riferimento cartesiano) che abbia quella terna come coordinate e identifichiamo la coppia (y₁,y₂) con il punto del piano z=0 di coordinate (y₁,y₂,0). Fatto questo, l'applicazione diventa la proiezione ortogonale di un punto dello spazio sul piano orizzontale z=0. Il nucleo è formato dai punti dell'asse z e la fibra sul punto (y₁,y₂) del codominio è formata dai punti (y₁,y₂,t) al variare di t. Questa fibra è dunque una retta parallela all'asse z. Osserviamo che Ker L è l'unica fibra che sia anche uno spazio vettoriale dato che le altre fibre non contengono il vettore nullo e quindi non possono essere un sottospazio vettoriale di R³.

Più in generale possiamo considerare la proiezione

che trasforma il vettore numerico (x₁,x₂,...,x_n,y₁,y₂,...,y_m) di R^n+m nel vettore numerico (y₁,y₂,...,y_m) di R^m. Anche questa applicazione, che si vede subito essere un morfismo, è suriettiva e il suo nucleo è formato dai vettori (x₁,x₂,...,x_n,y₁,y₂,...,y_m) tali che y₁=0,y₂=0,...,y_m=0. La sua dimensione è quindi n e una sua base è formata dai primi n vettori della base canonica di R^n+m. Di questa situazione non possiamo farci una immagine completa dato che gli spazi vettoriali che entrano in gioco possono essere di dimensione molto grande tuttavia possiamo immaginare la situazione cogliendone la sostanza con la nostra precedente terza figura: morfismo suriettivo e fibre infinite.

Il teorema di struttura permette di descrivere completamente le fibre di una applicazione lineare tra due spazi vettoriali di dimensione finita. Esse sono tutte essenzialmente uguali: sono "traslazioni" del nucleo. Abbiamo infatti il seguente

Teorema (sulle fibre di una applicazione lineare)
Sia L una applicazione lineare dello spazio vettoriale V nello spazio vettoriale W, sia w un vettore dell'immagine di L e v un qualunque vettore che abbia w come immagine. La fibra su w è allora data da

Dimostrazione
Osserviamo intanto che esiste un qualche vettore v tale che L(v)=w dato che, per ipotesi, w appartiene all'immagine di L. Scegliamo un tale vettore e supponiamo che v' sia un generico vettore della fibra L^-1(w), vogliamo dimostrare che, allora, esiste un vettore u del nucleo tale che v'=v+u, cioè, tale che v'-v appartiene al nucleo. Per verificare se v'-v appartiene al nucleo basta vedere se la sua immagine tramite L è zero. Abbiamo, essendo L lineare e dato che v e v' stanno nella stessa fibra:

L(v'-v)=L(v')-L(v) = w-w=0

Questo teorema ci dice essenzialmente che conoscendo il nucleo, per trovare i vettori di una particolare fibra L^-1(w) basta trovare un solo particolare vettore di quella fibra. Se infatti Ker L = Span(u₁,u₂, ... ,u_k) allora i vettori di L^-1(w) sono tutti e soli i vettori z della forma

z =v + a₁u₁ + a₂u₂ + ... + a_ku_k

al variare dei parametri a₁, a₂, ... ,a_k che possono essere scelti liberamente e indipendentemente uno dall'altro. In particolare i vettori di due diverse fibre possono essere messi in corrispondenza biunivoca tra loro. Possiamo dire che, se il nucleo è di dimensione k, le fibre, pur non essendo spazi vettoriali, sono tutte formate da ^k elementi. In particolare se Ker L = {0}, Ker L ha un solo elemento, e, di conseguenza, ogni fibra non vuota ha un solo elemento e, perciò l'applicazione è iniettiva. Abbiamo così queste importanti conseguenze del teorema di struttura

Corollario
Sia L una applicazione lineare dello spazio vettoriale V nello spazio vettoriale W, che supponiamo di dimensione finita. Allora

L è iniettiva se e solo se Ker L = {0}
L è suriettiva se e solo se dim W = dim V - dim Ker L

Dimostrazione
La prima parte del corollario deriva dal teorema sulle fibre, la seconda parte dal fatto che L è suriettiva se e solo se Im L = W e questo, per il teorema di struttura, è equivalente al fatto che dim W = dim Im L = dim V-dim Ker L.

Notiamo come sia il nucleo l'elemento determinate nello studio dei morfismi. Le 4 immagini precedenti con le quali abbiamo descritto intuitivamente i vari tipi di morfismi si ritrovano puntualmente in termini di nucleo dell'applicazione lineare: se il nucleo è nullo siamo nella situazione dei primi due disegni e il morfismo è iniettivo, altrimenti in quella dei due disegni successivi dove le fibre sono essenzialmente uguali tra loro e composte dalla stessa infinità di elementi del nucleo. I tre numeri dim V, dim W e dim Ker L sono in grado di descrivere qualitativamente ogni possibile morfismo tra spazi vettoriali di dimensione finita.

Esercizi