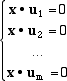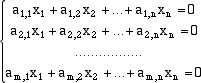|
XII 1. Spazio ortogonale a un dato sottospazio.
Consideriamo in tutto questo paragrafo uno spazio vettoriale V su R di dimensione finita con un prodotto scalare. Spazi di questo tipo sono tutti i sottospazi di
Rn o di uno spazio di vettori geometrici.
Sia U un sottospazio vettoriale di V. Si definisce lo spazio ortogonale di U il sottospazio
U i cui vettori sono tutti i vettori di V ortogonali ad ogni vettore di U. In simboli i cui vettori sono tutti i vettori di V ortogonali ad ogni vettore di U. In simboli
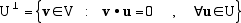
Lo spazio ortogonale è molto importante in vari contesti soprattutto perché si lega allo spazio delle soluzioni
di un sistema di equazioni lineari omogeneo. Consideriamo il caso particolarmente importante in cui V sia lo spazio Rn dei vettori numerici a n componenti col prodotto scalare canonico e siano u1, u2, ... , um m
vettori numerici a n componenti e sia
U = Span(u1, u2, ... , um)
allora lo
spazio ortogonale ad U è dato da tutti i vettori x = (x1,x2, ... , xn) tali che
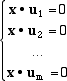
Se esplicitiamo il prodotto otteniamo un sistema lineare omogeneo di m equazioni in n incognite,
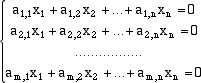
dove i coefficienti ai,j sono le componenti dei dati vettori ui. Ogni vettore x
dello spazio U ortogonale a U corrisponde a una soluzione del sistema lineare e viceversa ogni n-upla
di numeri che risolve il sistema da luogo a un vettore numerico ortogonale a U. Le soluzioni sono dunque tante quanti sono i vettori di
U ortogonale a U corrisponde a una soluzione del sistema lineare e viceversa ogni n-upla
di numeri che risolve il sistema da luogo a un vettore numerico ortogonale a U. Le soluzioni sono dunque tante quanti sono i vettori di
U cioé, se non c'è solo la soluzione nulla, sono infinite. Non è dunque possibile elencarle
tutte come si fa per le soluzioni di una ordinaria equazione ma, dato che queste soluzioni, come U cioé, se non c'è solo la soluzione nulla, sono infinite. Non è dunque possibile elencarle
tutte come si fa per le soluzioni di una ordinaria equazione ma, dato che queste soluzioni, come U ,
hanno la struttura di spazio vettoriale, possiamo esprimerle come combinazioni lineari di un numero finito di loro. Risolvere il sistema significa quindi
esplicitare il minor numero possibile di soluzioni in modo che ogni altra soluzione si possa ottenere come combinazione lineare di quelle.
Usando il linguaggio vettoriale il problema diventa quello di trovare una base esplicita di U ,
hanno la struttura di spazio vettoriale, possiamo esprimerle come combinazioni lineari di un numero finito di loro. Risolvere il sistema significa quindi
esplicitare il minor numero possibile di soluzioni in modo che ogni altra soluzione si possa ottenere come combinazione lineare di quelle.
Usando il linguaggio vettoriale il problema diventa quello di trovare una base esplicita di U cioè
il minor numero possibile di vettori che generano U cioè
il minor numero possibile di vettori che generano U . La dimensione di questo spazio di soluzioni,
che è
sempre finita perché è un sottospazio di Rn, esprime quante soluzioni indipendenti il sistema ammette: se r è
tale dimensione si dice anche, con una locuzione ottocentesca ma significatica, che il sistema ha infinito a r soluzioni, in simboli . La dimensione di questo spazio di soluzioni,
che è
sempre finita perché è un sottospazio di Rn, esprime quante soluzioni indipendenti il sistema ammette: se r è
tale dimensione si dice anche, con una locuzione ottocentesca ma significatica, che il sistema ha infinito a r soluzioni, in simboli
 r soluzioni. r soluzioni.
XII 2. Dimensione dello spazio ortogonale.
Torniamo ora allo studio di uno spazio vettoriale qualunque nel quale sia definito un prodotto scalare.
La considerazione delle basi ortonormali e l'algoritmo di Gram-Schmidt permettono di dimostrare un importante teorema che lega la
dimensione di U con quella di U. con quella di U.
Teorema XII 1
Sia V uno spazio vettoriale di dimensione finita dotato di un prodotto scalare e U un suo sottospazio. Risulta allora
dim U + dim U = dim V = dim V
Dimostrazione
A partire da un insieme di generatori di U costruiamo una sua base ortonormale (ad esempio con l'algoritmo di Gram-Schmidt). Sia
k= dim U e
{e1, e2, ... , ek} base ortonormale di U
completiamo questa base fino a trovare una base di V, cosa, come abbiamo visto,
sempre possibile e ortonormalizziamo questa base (ad esempio con l'algoritmo di Gram-Schmidt): sia dunque h+k = dim V e
{e1, e2, ... , ek, f1, f2, ... ,
fh}
base ortonormale di V
Osserviamo ora che i vettori f1, f2, ... ,fh sono vettori di
U linearmente indipendenti essendo ortogonali a ogni vettore della base di U. Quindi linearmente indipendenti essendo ortogonali a ogni vettore della base di U. Quindi
U 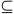 Span(f1,
f2, ... ,fh) Span(f1,
f2, ... ,fh)
D'altra parte i vettori f1, f2, ... ,fh generano
U . Se infatti v è un vettore di U . Se infatti v è un vettore di U , allora, essendo anche un vettore di V, posso scriverlo come combinazione lineare dei vettori della base di V, cioé , allora, essendo anche un vettore di V, posso scriverlo come combinazione lineare dei vettori della base di V, cioé
v = a1e1 + a2e2 + ... + akek +
b1f1 + b2f2 +... + bhfh
ma v è un vettore di U  dunque dunque
v.e1 = v.e2 = ... =
v.ek = 0
e quindi a1 = a1 = ... = ak = 0 e v risulta combinazione lineare dei vettori f
che quindi generano U . .
Notiamo che nel corso della dimostrazione abbiamo trovato una base ortonormale di V {e1, e2, ... , ek,
f1, f2, ... , fh} tale che
U = Span( e1, e2, ... , ek) e
U = Span(f1, f2, ... , fh) = Span(f1, f2, ... , fh)
ne segue che U + U = V e, come conseguenza della formula di Grassmann,
U = V e, come conseguenza della formula di Grassmann,
U  U U ={0}.
Il teorema precedente permette di "contare" le soluzioni di un sistema omogeneo di m equazioni lineari in n incognite: se le equazioni sono
indipendenti cioé se i vettori numerici a n componenti u1, u2, ... , um, sono
linearmente indipendenti allora esistono n-m soluzioni linearmente indipendenti dato che, in questo caso dim U = m e dim V = n. In generale per risolvere il
dato sistema e sapere quante sono le sue soluzioni indipendenti, si dovrà determinare la dimensione di U e ciò, partendo da un suo
sistema di generatori può essere fatto con l'algoritmo di Gram-Schimdt. L'algoritmo permette non solo di trovare la dimensione
di U ma anche una sua base ortonormale. Possiamo anche usare l'algoritmo per trovare una base ortonormale di tutto lo spazio V,
completando la base di U, i nuovi vettori che vengono calcolati generano lo spazio U ={0}.
Il teorema precedente permette di "contare" le soluzioni di un sistema omogeneo di m equazioni lineari in n incognite: se le equazioni sono
indipendenti cioé se i vettori numerici a n componenti u1, u2, ... , um, sono
linearmente indipendenti allora esistono n-m soluzioni linearmente indipendenti dato che, in questo caso dim U = m e dim V = n. In generale per risolvere il
dato sistema e sapere quante sono le sue soluzioni indipendenti, si dovrà determinare la dimensione di U e ciò, partendo da un suo
sistema di generatori può essere fatto con l'algoritmo di Gram-Schimdt. L'algoritmo permette non solo di trovare la dimensione
di U ma anche una sua base ortonormale. Possiamo anche usare l'algoritmo per trovare una base ortonormale di tutto lo spazio V,
completando la base di U, i nuovi vettori che vengono calcolati generano lo spazio U e dunque danno una base per lo spazio delle
soluzioni del sistema lineare omogeneo. Tuttavia esiste un altro algoritmo molto più semplice dal punto di vista computazionale perché non necessita
di operazioni irrazionali come l'estrazione di una radice quadrata ma si ottiene eseguendo sui coefficienti del sistema le sole operazioni
razionali di somma prodotto sottrazione e divisione. e dunque danno una base per lo spazio delle
soluzioni del sistema lineare omogeneo. Tuttavia esiste un altro algoritmo molto più semplice dal punto di vista computazionale perché non necessita
di operazioni irrazionali come l'estrazione di una radice quadrata ma si ottiene eseguendo sui coefficienti del sistema le sole operazioni
razionali di somma prodotto sottrazione e divisione.
J. C. F Gauss (1777-1855) a 56 anni
Questo algoritmo, che è quello oggi utilizzato dai calcolatori, è stato soperto da
Gauss nelle sue famose Disquisitiones cioé
nell'ambito della teoria dei numeri dove è molto importante sviluppare la teoria a prescindere da proprietà legate alla
continuità servendosi solo della struttura aritmetica dei numeri. L'algoritmo di Gauss, proprio per questo, permette di sviluppare una teoria
analoga alla
teoria degli spazi vettoriali, la teoria dei moduli, quando ci si restringe al caso nel quale tra gli scalari non è possibile eseguire sempre la
divisione come avviene, ad esempio nel caso dell'anello degli interi Z ={0, 1,-1,2,-2,3,-3, ... }.
Il calcolo esplicito della base dello spazio ortogonale può ancora
essere fatto
come vedremo, usando il metodo di Gauss. In questo modo, attraverso un calcolatore, che può gestire solo oggetti finiti, possiamo ugualmente
descrivere
le infinite soluzioni calcolando una base, che è sempre finita , dello spazio vettoriale U . .
L'operazione che associa ad ogni sottospazio di uno spazio vettoriale V di dimensione finita lo spazio ortogonale prefigura una sorta di
dualità tra l'operazione di somma e quella di intersezione: una somma si trasforma in una intersezione e una
intersezione in una somma. Precisamente
Teorema XII 2
Sia V uno spazio vettoriale di dimensione finita dotato di un prodotto scalare e siano U e W due suoi sottospazi.
Risulta allora
-
U
  = U = U
- Se
U
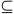 W allora
U W allora
U 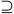 W W
- (U + W)
 = U = U 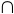 W
W
- (U
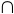 W) W) = U = U +
W +
W
Dimostrazione
Dimostriamo la prima formula. Scegliamo una base ortonormale di V in modo che risulti
U = Span( e1, e2, ... , ek) e
U = Span(f1, f2, ... , fh) = Span(f1, f2, ... , fh)
poiché, come risulta dalla decomposizione precedente, ogni vettore di U è ortogonale a ogni vettore di U abbiamo che ogni vettore di U è
un vettore di (U abbiamo che ogni vettore di U è
un vettore di (U ) ) . E viceversa. . E viceversa.
Dimostriamo la seconda formula. Supponiamo che W sia un sottospazio vettoriale di U e sia x
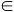 U U allora x.u = 0 per ogni u
allora x.u = 0 per ogni u 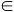 U e, in particolare essendo
W contenuto in U, x.u = 0 per ogni u U e, in particolare essendo
W contenuto in U, x.u = 0 per ogni u 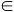 W. Ne segue che
x W. Ne segue che
x 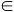 W W . .
Dimostriamo la terza formula dimostrando la doppia inclusione. Intanto risulta
(U + W) 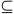 U U 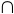 W
W infatti se x infatti se x 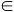 (U + W) (U + W) allora
x.(u + w) = 0 u allora
x.(u + w) = 0 u 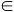 U e
per ogni w U e
per ogni w 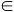 W. In particolare
x.(u + 0) = 0 per ogni u W. In particolare
x.(u + 0) = 0 per ogni u 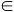 U quindi
x U quindi
x 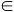 U U ma anche
x.(0 + w) = 0 per ogni w ma anche
x.(0 + w) = 0 per ogni w 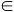 W quindi
x W quindi
x 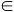 W W . x appartiene dunque a U . x appartiene dunque a U 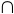 W
W . L'inclusione inversa si dimostra nella medesima maniera. . L'inclusione inversa si dimostra nella medesima maniera.
L'ultima relazione segue dalle precedenti. Infatti
(U 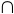 W) W)  = U = U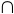 W
e (U W
e (U + W + W ) ) =
U =
U 
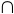 W W  = U
= U 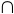 W e, dalla seconda formula, segue che
due sottospazi vettoriali sono uguali se e solo se hanno lo stesso ortogonale. W e, dalla seconda formula, segue che
due sottospazi vettoriali sono uguali se e solo se hanno lo stesso ortogonale.
Esercizi
| |