Vogliamo determinare, a partire da questi vettori una base per lo spazio U ortogonale a U. Fissiamo una base ortonormale di V e siano {e₁, e₂, ... , e_n} i vettori di questa base. Possiamo allora esprimere i generatori di U come combinazioni lineari dei vettori della base ortonormale:

Ora, se x = x₁e₁ + x₂e₂ + ... + x_ne_n è un generico vettore di V, allora x appartiene a U se e solo se è ortogonale a ogni vettore di U, ed essendo U generato dai vettori u₁, u₂, ... , u_m questo è equivalente al fatto che x sia ortogonale ai vettori u_i per ogni i=1,2,...m cioé che

dato che, essendo e₁, e₂, ... , e_n una base ortonormale di V, i prodotti e_i.e_j sono tutti nulli tranne nel caso in cui i=j, caso in cui il prodotto fa 1.
Il vettore x è dunque un vettore dello spazio U se e solo se le sue componenti (x₁,x₂, ... , x_n) soddisfano il seguente sistema omogeneo di m equazioni lineari in n incognite:

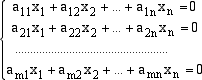Viceversa lo spazio delle soluzioni di un sistema omogeneo di m equazioni lineari in n incognite si interpreta come il sottospazio di Rⁿ ortogonale allo spazio generato dai vettori numerici le cui n componenti siano i coefficienti delle m equazioni. Precisamente a partire dal sistema omogeneo precedente, possiamo costruire i vettori numerici

e, per come è definito il prodotto scalare in Rⁿ, lo spazio ortogonale a U = Span(u₁,u₂, ... , u_m) è proprio lo spazio delle soluzioni del sistema lineare precedente.

Osserviamo ora che, in generale, se lo spazio U viene generato con altri vettori, magari più semplici dei vettori dai quali siamo partiti, se cioè

dove i nuovi vettori v_i sono dati da

il nuovo sistema da risolvere diventa: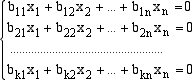

e le soluzioni dell'uno sono le stesse delle soluzioni dell'altro dato che esse rappresentano i vettori dello stesso spazio U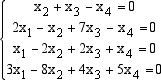. Il vantaggio è ora che il nuovo sistema, se è ridotto (cioè se la matrice dei suoi coefficenti è ridotta) si lascia risolvere con estrema facilità.

Esempio
Siano u₁ = (0,1,1,-1), u₂ = (2,-1,7,-1), u₃ = (1,-2,2,1), u₄ = (3,-8,4,5) quattro vettori numerici di R⁴ e sia U = Span(u₁, u₂, u₃, u₄). Vogliamo calcolare la dimensione di U e una sua base.
La questione si riduce a risolvere il sistema di equazioni

Queste equazioni traducono infatti la condizione che i vettori x che cerchiamo siano ortogonali ai 4 vettori u_i che generano lo spazio U. Riduciamo ora, con l'algoritmo di Gauss, la matrice che ha come righe le componenti dei 4 vettori dati:

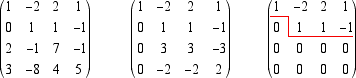Poniamo v₁ = (1,-2,2,1), v₂ = (0,1,1,-1). Tali vettori sono una base per U che risulta uguale a Span(v₁, v₂) e il sistema iniziale ha le stesse soluzioni del sistema molto più semplice

Per risolvere questo sistema prendiamo x₃ e x₄ come variabili libere, alle quali possiamo dare dei valori arbitrari ed esprimiamo le altre variabili x₁ e x₂ in funzione di queste a partire dal basso. Poniamo allora, ad esempio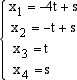

Usando i vettori numerici (colonna) possiamo esprimere le soluzioni nella forma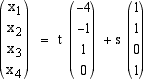

Chiamando w₁ = (-4,-1,1,0), w₂ = (1,1,0,1), abbiamo che ogni vettore x ortogonale a U si scrive nella forma x = t w₁ + sw₂ inoltre w₁ e w₂ sono linearmente indipendenti e

U = Span(w₁, w₂)

è un sottospazio vettoriale di R⁴ di dimensione 2.

Notiamo che la stessa procedura che abbiamo indicato in questo esempio si applica per risolvere un qualunque sistema omogeneo di m equazioni in n incognite. Le soluzioni del sistema non cambiano facendo operazioni elementari sulle righe della matrice dei suoi coefficenti e il sistema si riduce, alla fine dell'algoritmo di Gauss, a un sistema ridotto che può essere risolto facilmente: si attribuiscono valori arbitrari alle variabili libere che sono quelle il cui coefficente non è un pivot, e si risolve il sistema dal basso a partire dall'ultima equazione sostituendo i valori trovati nella equazione precedente fino ad arrivare alla prima equazione, come abbiamo fatto nell'esempio precedente. Ricapitolando quanto abbiamo dedotto, abbiamo che

• il numero r dei pivot è uguale alla dimensione di U
• il numero di variabili liberi è uguale a n-r cioè al numero di incognite meno il numero dei pivot
La dimensione dello spazio delle soluzioni U è uguale a n-dim U (teorema sulla dimensione dello spazio ortogonale)

Da tutto questo ricaviamo che la dimensione dello spazio delle soluzioni è uguale al numero di variabili liberi. Il concetto generale di dimensione si lega, come si vedrà in corsi più avanzati, all'idea di gradi di libertà e nel caso specifico che abbiamo considerato questa idea acquista un significato preciso e ben chiaro: dire che le soluzioni di un sistema lineare omogeneo sono ^k, come veniva detto nel secolo XIX significa che le soluzioni dipendono da k variabili libere che possono essere scelte arbitrariamente indipendentemente una dall'altra e questo nel linguaggio di oggi si esprime dicendo che lo spazio vettoriale delle soluzioni del sistema ha dimensione k. Il teorema seguente riassume quanto detto.

Teorema
L'insieme delle soulzioni di un sistema omogeneo di m equazioni lineari in n incognite è uno spazio vettoriale di dimensione n-r essendo r m il rango per righe della matrice dei coefficenti del sistema.

Concludiamo questo paragrafo applicando la nostra teoria ad un problema significativo e non banale: la descrizione di tutti i quadrati magici 4x4. Ricordiamo che un quadrato magico 4x4 è una tabella di numeri

dove la somma dei numeri su ogni riga ogni colonna e ogni diagonale è lo stesso. Dato che la somma di quadrati magici e il prodotto per uno scalare si esegue sulle singole componenti, possiamo identificare un quadrato magico con un vettore numerico x a 16 componenti. Lo spazio V dei quadrati magici di ordine 4 risulta così un sottospazio vettoriale di R¹⁶. Naturalmente un vettore x appartiene a V se e solo se le sue componenti verificano le condizioni che definiscono il quadrato magico cioé se e solo se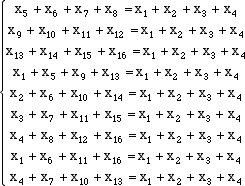

Si tratta dunque di risolvere un sistema di equazioni lineari omogeneo di 9 equazioni in 16 incognite. La matrice A del sistema è la matrice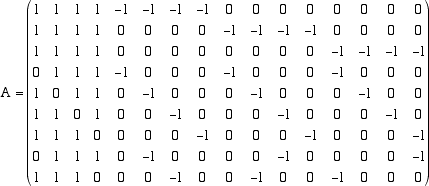

Si tratta ora di ridurre la matrice con l'algoritmo di Gauss facendo trasformazioni elementari sulle righe. Alla fine del calcolo si trova la seguente matrice ridotta con i relativi pivot cerchiati in rosso.

La matrice ha rango 8 e quindi la dimensione dello spazio V è data da 16-8 = 8. Per trovare una base di V dobbiamo risolvere il sistema ridotto individuando le 8 variabili libere e partendo dall'ultima equazione. Guardando la matrice si vede che le variabili libere sono x₈, x₁₀, x₁₁ x₁₂, x₁₃, x₁₄, x₁₅, x₁₆. Risolvendo il sistema dal basso, chiamando t₁, t₂, t₃, t₄, t₅, t₆, t₇, t₈ le 8 variabili libere, abbiamo per le ultime 9 incognite, i valori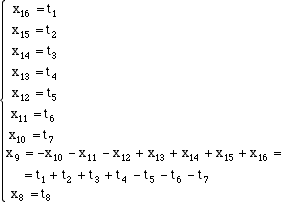

continuando a risolvere le equazioni dal basso troviamo

e dunque

Con calcoli analoghi troviamo

Il coefficiente di t₁ nelle 12 variabili fornisce il primo vettore della base che stiamo cercando: abbiamo

analogamente per gli altri

Gli 8 vettori che abbiamo trovato sono una base per lo spazio delle soluzioni del sistema e ogni soluzione x si esprime come loro combinazione linare

Scrivendo i vettori che abbiamo trovato come quadrati magici possiamo dire che ogni quadrato magico di ordine 4 si esprime in modo unico come combinazione lineare degli 8 quadrati magici rappresentati, nell'ordine, nella figura seguente.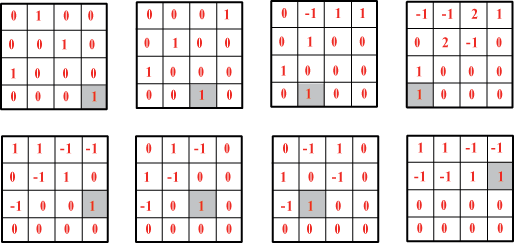

E' immediato verificare, a riprova, che questi 8 diagrammi sono quadrati magici di ordine 4 linearmente indipendenti, infatti la posizione grigia, in ogni quadrato, è nulla in tutti gli altri 7. In particolare, a partire da questa base, è facile scrivere un dato quadrato come combinazione lineare di questi: il coefficiente di u₁ sarà quello in basso a sinistra (x₁₆), il coefficiente di u₂ sarà x₁₅ ecc. ecc. In particolare il quadrato d di Durer si scrive

Esercizi